Oscillating stars can be found almost everywhere in the HR diagramme:
Schematic location of various classes of pulsating stars in the HR diagramme. The solid lines show
evolutionary tracks for stars of masses (from the top) of 20, 12, 7, 4, 3, 2 and 1 solar masses (click figure to enlarge).
Measurement of a set of
oscillation frequencies enables us to infer their internal structure
and hence state of evolution. Each frequency senses a different
weighted function of the stellar interior. A set of frequencies can
yield detailed knowledge of the internal structure, enabling us to
deduce the state of evolution and hence the age.
The power of such analyses has been forcefully demonstrated in the solar case, where helioseismology has provided dramatic insight into the properties of the solar interior. Through inversion of extensive sets of frequencies it has been possible to determine the sound speed in most of the Sun, hence testing in detail models of solar structure. This has revealed anomalies below the outer convective zone and just outside the solar core, and also allowed investigation of subtle features of the thermodynamic properties of matter in the Sun, as well as a precise determination of the solar envelope helium abundance. The general agreement between the inferred structure of the solar core and normal solar models strongly indicates that the solution to the solar neutrino problem must result from previously unsuspected properties of the neutrinos, rather than deficiencies in the solar models. Analyses of frequency splittings have yielded detailed determinations of the internal angular velocity. Many of these results are based on the excellent observations obtained from the ESA/NASA SOHO mission.
In contrast to helioseismology, seismology of distant stars is restricted to low-degree modes, but it is just these modes that penetrate into the deep interior and therefore convey information on the interior structure and state of evolution. Furthermore, the comparatively limited set of modes accessible in stars is compensated by the richness of stellar properties that may be investigated, far beyond the properties of the solar interior, such as
the mass and radii of convective cores, rapid rotation and the variation with mass and chemical composition. This will, for example, allow detailed investigations of the uncertain mixing processes associated with convective cores in main-sequence stars, of great importance to their subsequent evolution.
Members of open clusters present a specific interest. Their uniform chemical composition and age, and nearly common distance, provide very stringent constraints on the modeling, increasing the information obtained from the oscillation frequencies. In young clusters, we may in particular observe the beta Cephei stars, and bring important constraints on the evolution of massive stars. In the older clusters, oscillations in sub-giants (similar to those observed in eta Bootis can be studied. Therefore, the asteroseismic analysis of members of open clusters chosen to sample an age sequence, will allow us to constrain severely stellar evolution modeling.
Also, the properties of the metal-poor stars (Pop. II stars) are of great interest; these are expected to be amongst the oldest in the Galaxy, often similar to the stars that are used for age determinations of globular clusters, and may provide important limits on the age of the Galaxy and, by implication, the Universe.
The modes of oscillation can be conveniently represented in terms of surface harmonics Ylm , radial eigenfunctions
and oscillation
frequencies 
where n is the order of the mode
(approximately the number of nodes in the radial direction), and l is the degree, determining
the overall horizontal scale. For a spherical star the azimuthal order m is degenerate, the degeneracy
being lifted by a non-radial perturbation, e.g. rotation. A typical mode
is represented in the following figure:
Example of a non-radial oscillation mode with l =2, m=2, n=18.
This simulation of the pulsating star illustrates the surface behaviour
of the mode, determined by the relevant spherical harmonic,
as well as the behaviour in the interior which is shown in the cut-out.
Note that the amplitude is substantial even in the central region of the star,
reflecting the sensitivity of the oscillation frequencies to the core structure
(click figure to enlarge)
The relation between the frequencies and the internal properties of the star is reasonably well understood; based on this understanding one can isolate information about particular properties of the star, or regions within it, by suitably combining the frequencies.
Low-degree acoustic modes accessible for distant stars probe their central regions. Even more sensitive probes of the core are obtained where g modes can be observed. Important goals of the analysis are evidently to determine the overall parameters of the stars. In particular, the stellar ages, particularly important in the framework of PLATO, since their measurement will allow us to estimate the ages of the detected planets, can be determined as a result of the sensitivity of the frequencies to the structure of stellar cores. At a more fundamental level, the asteroseismic data can be used to investigate the complex physics that determine stellar structure and evolution; this will not only improve the calculations of stellar models but will also enable us to utilize the observations to learn about physics of matter under extreme conditions.
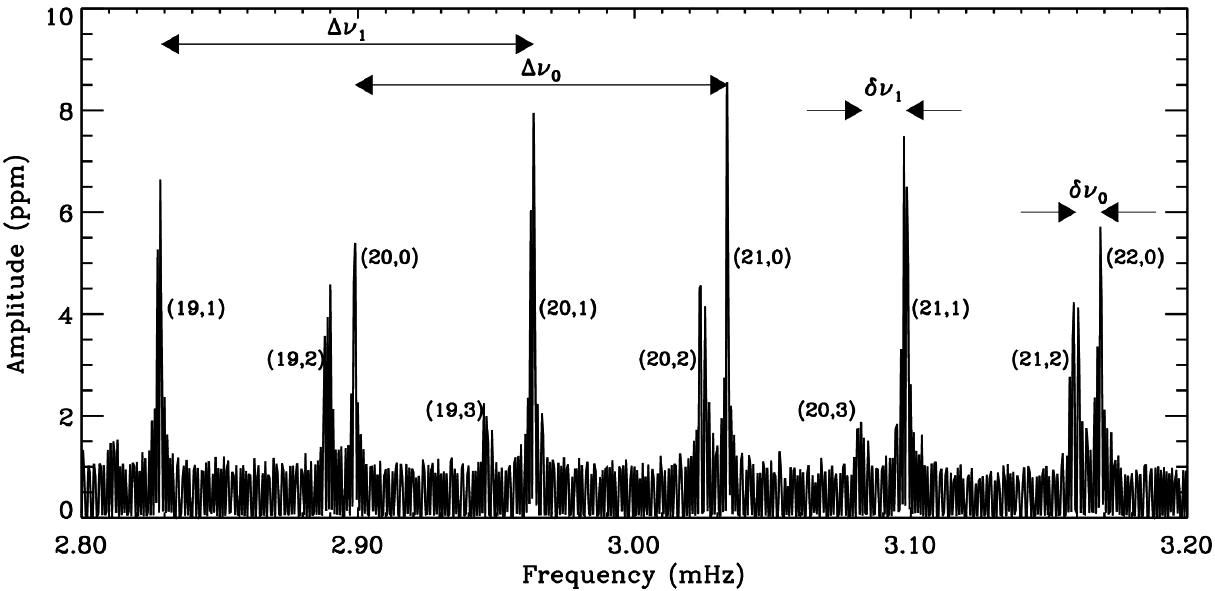
Amplitude spectra of solar oscillations measured by the VIRGO instrument on SOHO.
The figure shows only a portion of the solar oscillation spectrum, illustrating the details
of the definition of the "large'' and "small separations''. Each frequency peak is labelled
with the n, l values of the oscillation mode (click figure to enlarge)
These
two numbers alone give significant constraints. The average large
separation contains information on the mean properties of the star, e.g. its
mean density, while the average small separation is sensitive to the chemical composition in the central regions, and can therefore measure the central hydrogen content, hence the age of the star.
In addition to the simple use of the asymptotic behaviour of stellar oscillations described by the large and small separation, a complete inversion of all measured mode frequencies can be performed to determine the internal structure of stars. Such inversion techniques have been developed and successfully applied in terrestrial and solar seismology where the measured set of frequencies span a large range of n, l values. New techniques have been developed which are applicable to data sets with only low l values -- such as would be obtained with PLATO. These techniques have been extensively described in the recent literature, and are not discussed in detail here.
Rotation removes the m degeneracy in the frequencies; the resulting m-dependence of the frequencies permits the determination of the internal angular velocity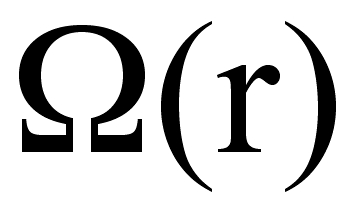
inside the star, as a function of r.
The measurement of the so-called rotational splitting, i.e. the difference between
frequencies with the same n, l but
different m, for different
values of n, can be used to
infer the internal rotation rate and its variation with radius. An
example of what can be achieved is presented in Lochard et
al. (2005), who considered a model of an evolved 1.5 solar mass
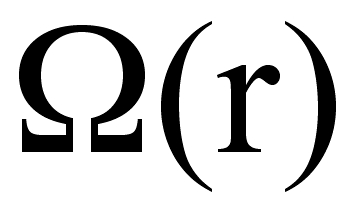star with a prescribed and a surface
rotational velocity of 30 km s-1, and showed that inversion
of the frequency splittings for an assumed rotation profile reproduced
the input rotation profile to excellent accuracy, with frequency
measurement accuracies typical of what is expected from CoRoT, ranging
from 0.05 to 0.22 micro-Hz, depending on the mode lifetime.
The power of such analyses has been forcefully demonstrated in the solar case, where helioseismology has provided dramatic insight into the properties of the solar interior. Through inversion of extensive sets of frequencies it has been possible to determine the sound speed in most of the Sun, hence testing in detail models of solar structure. This has revealed anomalies below the outer convective zone and just outside the solar core, and also allowed investigation of subtle features of the thermodynamic properties of matter in the Sun, as well as a precise determination of the solar envelope helium abundance. The general agreement between the inferred structure of the solar core and normal solar models strongly indicates that the solution to the solar neutrino problem must result from previously unsuspected properties of the neutrinos, rather than deficiencies in the solar models. Analyses of frequency splittings have yielded detailed determinations of the internal angular velocity. Many of these results are based on the excellent observations obtained from the ESA/NASA SOHO mission.
In contrast to helioseismology, seismology of distant stars is restricted to low-degree modes, but it is just these modes that penetrate into the deep interior and therefore convey information on the interior structure and state of evolution. Furthermore, the comparatively limited set of modes accessible in stars is compensated by the richness of stellar properties that may be investigated, far beyond the properties of the solar interior, such as
the mass and radii of convective cores, rapid rotation and the variation with mass and chemical composition. This will, for example, allow detailed investigations of the uncertain mixing processes associated with convective cores in main-sequence stars, of great importance to their subsequent evolution.
Members of open clusters present a specific interest. Their uniform chemical composition and age, and nearly common distance, provide very stringent constraints on the modeling, increasing the information obtained from the oscillation frequencies. In young clusters, we may in particular observe the beta Cephei stars, and bring important constraints on the evolution of massive stars. In the older clusters, oscillations in sub-giants (similar to those observed in eta Bootis can be studied. Therefore, the asteroseismic analysis of members of open clusters chosen to sample an age sequence, will allow us to constrain severely stellar evolution modeling.
Also, the properties of the metal-poor stars (Pop. II stars) are of great interest; these are expected to be amongst the oldest in the Galaxy, often similar to the stars that are used for age determinations of globular clusters, and may provide important limits on the age of the Galaxy and, by implication, the Universe.
The modes of oscillation can be conveniently represented in terms of surface harmonics Ylm , radial eigenfunctions
and oscillation
frequencies where n is the order of the mode
(approximately the number of nodes in the radial direction), and l is the degree, determining
the overall horizontal scale. For a spherical star the azimuthal order m is degenerate, the degeneracy
being lifted by a non-radial perturbation, e.g. rotation. A typical mode
is represented in the following figure:Example of a non-radial oscillation mode with l =2, m=2, n=18.
This simulation of the pulsating star illustrates the surface behaviour
of the mode, determined by the relevant spherical harmonic,
as well as the behaviour in the interior which is shown in the cut-out.
Note that the amplitude is substantial even in the central region of the star,
reflecting the sensitivity of the oscillation frequencies to the core structure
(click figure to enlarge)
The relation between the frequencies and the internal properties of the star is reasonably well understood; based on this understanding one can isolate information about particular properties of the star, or regions within it, by suitably combining the frequencies.
Low-degree acoustic modes accessible for distant stars probe their central regions. Even more sensitive probes of the core are obtained where g modes can be observed. Important goals of the analysis are evidently to determine the overall parameters of the stars. In particular, the stellar ages, particularly important in the framework of PLATO, since their measurement will allow us to estimate the ages of the detected planets, can be determined as a result of the sensitivity of the frequencies to the structure of stellar cores. At a more fundamental level, the asteroseismic data can be used to investigate the complex physics that determine stellar structure and evolution; this will not only improve the calculations of stellar models but will also enable us to utilize the observations to learn about physics of matter under extreme conditions.
The oscillation frequencies of a
star exhibit some regular patterns
which allow diagnostic information on specific characteristics of the
stellar structure to be derived, even in the presence of low S/N data. This regularity can be
clearly seen in the solar spectrum shown below: the main characteristic
of this spectrum is the approximately equal "large separation'' 
of approximately135
microHz between the larger peaks corresponding to p modes with (n, l) and (n-1, l), but important information
is
also encoded in the "small separation'' 
between peaks with
nearly the same frequency corresponding to p modes with (n, l) and (n-1, l+2).
of approximately135
microHz between the larger peaks corresponding to p modes with (n, l) and (n-1, l), but important information
is
also encoded in the "small separation'' between peaks with
nearly the same frequency corresponding to p modes with (n, l) and (n-1, l+2).Amplitude spectra of solar oscillations measured by the VIRGO instrument on SOHO.
The figure shows only a portion of the solar oscillation spectrum, illustrating the details
of the definition of the "large'' and "small separations''. Each frequency peak is labelled
with the n, l values of the oscillation mode (click figure to enlarge)
mean density, while the average small separation is sensitive to the chemical composition in the central regions, and can therefore measure the central hydrogen content, hence the age of the star.
In addition to the simple use of the asymptotic behaviour of stellar oscillations described by the large and small separation, a complete inversion of all measured mode frequencies can be performed to determine the internal structure of stars. Such inversion techniques have been developed and successfully applied in terrestrial and solar seismology where the measured set of frequencies span a large range of n, l values. New techniques have been developed which are applicable to data sets with only low l values -- such as would be obtained with PLATO. These techniques have been extensively described in the recent literature, and are not discussed in detail here.
Rotation removes the m degeneracy in the frequencies; the resulting m-dependence of the frequencies permits the determination of the internal angular velocity
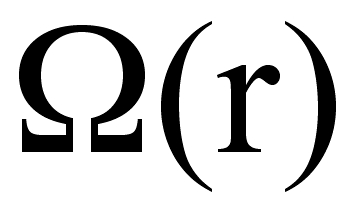inside the star, as a function of r.
The measurement of the so-called rotational splitting, i.e. the difference between
frequencies with the same n, l but
different m, for different
values of n, can be used to
infer the internal rotation rate and its variation with radius. An
example of what can be achieved is presented in Lochard et
al. (2005), who considered a model of an evolved 1.5 solar mass
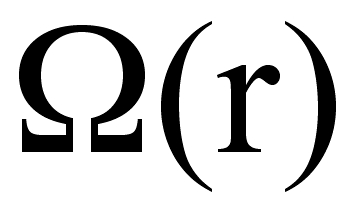star with a prescribed and a surface
rotational velocity of 30 km s-1, and showed that inversion
of the frequency splittings for an assumed rotation profile reproduced
the input rotation profile to excellent accuracy, with frequency
measurement accuracies typical of what is expected from CoRoT, ranging
from 0.05 to 0.22 micro-Hz, depending on the mode lifetime.