On February 8, 1992, Ulysses crossed the Io plasma torus (IPT).
That spacecraft carried Unified Radio and Plasma Waves (URAP) receivers
[Stone et al., 1992a], including a low-frequency
receiver sweeping the frequency range 1.25 to 48.5 kHz in 128 s with
a resolution of 0.75 kHz. Many spectra were thus recorded which showed,
between consecutive gyroharmonic frequencies, weakly banded emissions
characterized by a large bandwidth and a low intensity, which varied
smoothly in both time and frequency.
All these spectra were modulated by the spacecraft spin in
Jupiter's magnetic field. Since the onboard particle analyzers were
turned off, these wave measurements are the only ones allowing us to obtain an
in situ plasma diagnostics in the IPT. Moreover,
the Ulysses trajectory was basically north to south in the IPT, and so most of
these spectra were acquired over a large latitude interval (i.e., a distance
from the torus equator in the range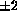 
)
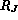and a small variation (from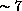 
to
8 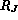) of the Jovicentric distance. It is the first time one can get such
in situ measurements, because previous spacecraft remained close to the equator
at this distance to Jupiter (see [Hoang et al., 1993] for
comparison between Ulysses and Voyager 1 data).
The above mentioned emissions have already been studied by
[Meyer-Vernet, Hoang and Moncuquet, 1993], who interpreted them as
quasi-thermal fluctuations in Bernstein waves and proposed to deduce the
temperature from their apparent polarization. Bernstein waves [Bernstein, 1958]
are electrostatic waves which propagate ideally without
damping, perpendicular to the magnetic field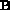 
; their wavelength
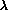is of the order of 
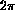times the electron gyroradius. Since the
angular receiving pattern of an electric antenna is very sensitive to the
wavelength 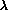when it becomes comparable to the antenna length L,
the polarization measured with a
spinning antenna is thus very sensitive to 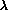. The condition 
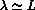is realized in the IPT. [Meyer-Vernet, Hoang and Moncuquet, 1993]
showed that this polarization shifts by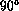 
for a certain value of the wavelength, which can thus be evaluated from the
data, yielding the electron gyroradius and, from it, the electron temperature.
Using that method, [Hoang et al., 1993] published temperature
measurements with a 40% uncertainty.
In the present paper, we generalize that method: we no longer
limit ourselves to measuring 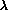when the polarization shifts by .
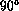We systematically fit the antenna angular response to each full modulation
period thus using many more of the available data and proving the
self-consistency of our results.
For each of
about 80 available spectra, we obtain from 3 to 12 points on the dispersion
curve of the electrostatic waves in the ambient plasma. Note that this
method only uses one available dipole antenna, contrary to the usual
methods of comparing the amplitudes on two different antennas [see
[Filbert and Kellogg, 1988]] or making correlations
between several wave components [see [Lefeuvre et al., 1992]].
Having measured the dispersion curves, we have to deal with two
different situations.
In the more common
one, the local plasma frequency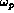 
is measured independently
[Hoang et al., 1993]. In that case,
we can calculate the dispersion
relation for Bernstein waves in a Maxwellian electron plasma of known
density (appendix B). We then fit the solution of the theoretical
dispersion equation to our experimental points with the electron
temperature as the only free parameter which is thus determined
to within 15 to 25%.
The main purpose of this paper is to describe the new method of obtaining the
electron temperature; we thus only show, without further discussions, the
temperature obtained in the IPT. It is noteworthy that the good precision
obtained with that method
made possible a quantitative analysis of the IPT latitudinal
variation: this is done in a related paper in which we propose new
interpretations and constraints about the previous IPT models [Meyer-Vernet, Moncuquet and Hoang, 1995].
In the few cases when no measurements of the density are available,
we have
to fit the theoretical dispersion curves to our data points with two free
parameters, the temperature and the density, which can then be estimated with
an uncertainty of only 40 to 50%.
Finally we discuss the physical relevance of our temperature
determination, especially in the case of a non-Maxwellian velocity
distribution.