

Next: 0.1.4 Linéarisation des équations
Up: 0.1 Fluides classiques et
Previous: 0.1.2 Cas d'un fluide
Le fluide est dit parfait lorsque les effets de viscosité peuvent être
négligés: la loi de comportement (3) est alors réduite à
 |
(10) |
Les équations du mouvement s'écrivent:
 |
(11) |
et sont appelées ``équations d'Euler''.
Cas incompressible, homogène
Dans ce cas, il faut ajouter comme précédemment :
 |
(12) |
Les cinq relations (11) et (12) permettent avec
des conditions aux limites adéquates, la détermination des inconnues
 et celle de la pression à une constante près.
et celle de la pression à une constante près.
Fluide compressible barotrope
Si le fluide est compressible, (12) est remplacé par
 |
(13) |
il faut donc une information supplémentaire: par exemple le fluide
peut être barotrope, c'est-à-dire qu'il existe une loi d'état
 de nature thermodynamique reliant la pression à la densité
du milieu. Ce type de loi englobe en particulier les deux cas
classiques:
de nature thermodynamique reliant la pression à la densité
du milieu. Ce type de loi englobe en particulier les deux cas
classiques:
-
 d'un gaz parfait à chaleur spécifique
constante en évolution isotherme.
d'un gaz parfait à chaleur spécifique
constante en évolution isotherme.
-
 d'un gaz parfait à chaleur spécifique
constante en évolution adiabatique.
d'un gaz parfait à chaleur spécifique
constante en évolution adiabatique.
Les conditions aux limites (4),(5) sont dans ce cas
surabondantes; il faut tenir compte ici du fait que l'ordre des
dérivées des équations du mouvement est passé de deux à un avec la
disparition du Laplacien de  . On se contentera de la
condition (condition de glissement sur une paroi fixe
. On se contentera de la
condition (condition de glissement sur une paroi fixe  limitant
le volume
limitant
le volume 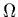 ):
):
 |
(14) |


Next: 0.1.4 Linéarisation des équations
Up: 0.1 Fluides classiques et
Previous: 0.1.2 Cas d'un fluide
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
![]() . On se contentera de la
condition (condition de glissement sur une paroi fixe
. On se contentera de la
condition (condition de glissement sur une paroi fixe ![]() limitant
le volume
limitant
le volume ![]() ):
):