Quelques relations entre puissances de nombres entiers

Le triangle égyptien et ses avatars :

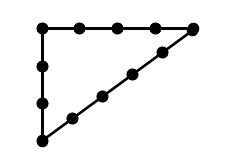
Pour tracer au sol les contours à angles droits des murs des bâtiments à ériger, les anciens égyptiens utilisent une corde refermée sur elle-même et sur laquelle 12 segments équidistants sont marqués, par exemple par des nœuds qu’on numérotera 1, 2, 3, .., 12 . Si on cherche à former un triangle en tendant la corde entre les points 1, 4 et 8, en créant donc des segments de longueur a = 3, b = 4 et c = 5, on obtient nécessairement un triangle rectangle. Il satisfait en effet bien au théorème de Pythagore : a² + b² = c² car on a bien l’égalité diophantienne 3² + 4² = 9 + 16 = 25 = 5²

D’autres triangles rectangles dont les côtés ont des longueurs multiples entiers d’un segment unitaire existent ; par exemple [5, 12, 13]

Ce problème s’énonce ainsi : peut-on trouver 2 ensembles {a₁,…,a_n} et {b₁,…,b_n} d’entiers tels que
a₁^m +…+ a_n^m = b₁^m +…+ b_n^m pour m = 1,…,k ?
En abrégé, le problème est noté : {a_i}=^k= {b_i} et les solutions sont appelées multigrades

Le problème possède bien des solutions et, par exemple, Euler et Goldbach montrent en 1750 que
{a, b, c, a+b+c} =²= {a+b, b+c, c+a}

Cette suite se construit très simplement en considérant 2 symboles complémentaires (par exemple a et b, ou + et -, ou 0 et 1). Etant donné le terme S_n, on construit le terme S_n+1 en concaténant au terme S_n son complémentaire (a => b et b => a).
On part du premier terme de la suite: S₀ = a qui donne : S₁ = ab, puis S₂ = ab ba, et ainsi de suite :
S3 = ab ba ba ab,
S4 = ab ba ba ab ba ab ab ba
…..
Cette suite possède la propriété de ne pas être périodique (on ne trouve pas de motif qui se répète régulièrement) et d’avoir un caractère fractal. Elle est dotée d’un véritable don d’ubiquité car elle apparaît dans de très nombreux problèmes qui n’ont en principe aucun points communs entre eux.

Prouhet montre en 1851 que cette suite (elle n’a alors bien sûr pas ce nom) permet de construire une solution multigrade au problème de Prouhet-Tarry-Escott pour n = 2^N et k = N

Cette solution consiste à prendre pour les a_i les rangs des “a” dans le terme d’ordre N de la série de P-T-M et pour les b_i les rangs des “b”
Ainsi le terme d’ordre 3 qui s'écrit ab ba ba ab ba ab ab ba, donne :
{a_i} = {1,4,6,7,10,11,13,16} et {b_i} = {2,3,5,8,9,12,14,15} et on vérifie bien que
{1,4,6,7,10,11,13,16} =³= {2,3,5,8,9,12,14,15}
autrement dit :
1 + 4 + 6 + 7 + 10 + 11 + 13 + 16 = 2 + 3 + 5 + 8 + 9 + 12 + 14 + 15
1² + 4² + 6² + 7² + 10² + 11² + 13² + 16² = 2² + 3² + 5² + 8² + 9²+ 12² + 14² + 15²
1³ + 4³ + 6³ + 7³ + 10³ + 11³ + 13³ + 16³ = 2³ + 3³ + 5³ + 8³ + 9³+ 12³ + 14³ + 15³
C'est un résultat assez fascinant quand on réalise que quelque soit k, on peut toujours trouver deux ensembles d'entiers, tous différents, tels que toutes les sommes de leurs éléments élevés à une puissance entre 0 et k soient égales.
On aurait pu tout aussi bien faire commencer la suite des entiers non pas à 1 mais à une valeur quelconque J, car en effet (J + i)^k = J^k + k J^(k-1)i + k(k-1)/2 J^(k-2) i² + ... + i^k : on fait bien apparaître toutes les sommes i^k, i^k-1, i^k-2, etc. qui vérifient chacune la propriété de Prouhet. La propriété de Prouhet est donc invariante par translation.
Une application originale est la découpe d'un saucisson de la façon la plus égale possible entre deux convives...

Prouhet va plus loin : il montre que la suite de m^k entiers qui se suivent peut être partitionnée en m sous-ensemble {a_1,i}, {a_2,i}, …, {a_m,i} qui vérifient :
{a_1,i} =^k= {a_2,i} =^k= … =^k= {a_m,i}
C’est une suite de P-T-M généralisée qui permet de définir les sous-ensembles. Elle se construit en appliquant la règle suivante : prendre le terme courant, faire subir à ses éléments toutes les permutations circulaires, les concaténer.
Ainsi si m = 3 :
abc => abc bca cab => abc bca cab bca cab abc cab abc bca
On obtient alors le multigrade en considérant le terme d’ordre k de cette suite, en prenant comme a_i les rangs des “a”, comme b_i les rangs des “b”, comme c_i les rangs des “c”, etc.
Soit pour l’exemple précédent :
{1,6,8,12,14,16,20,22,27} =²= {2,4,9,10,15,17,21,23,25} =²= {3,5,7,11,13,18,19,24,26}
Du coup, la découpe d'un saucisson de la façon la plus égale possible entre k convives devient également possible !