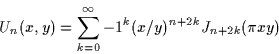Next: 3.2 Discussion
Up: 3. MODELING A REALISTIC
Previous: 3. MODELING A REALISTIC
The light emitted by a point source (assumed to be at the infinity to yield
planar waves) incident on a sharp-edged obstacle (such as a KBO) is
diffracted. Owing to the Huygens-Fresnel principle of wave
propagation, each
point of a wave front may be considered as the center of a secondary
disturbance giving rise to spherical wavelets, which mutually interfere. If
part of the original wave front is blocked by an obstacle, the system of
secondary waves is incomplete, so that diffraction occurs. When observed at a
finite distance D from the obstacle, this effect is known as ``Fresnel
diffraction'', and falls within the scope of the Kirchhoff diffraction theory
which remains valid as long as the dimensions of the diffracting obstacles are
large compared to the observed wavelength 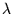 and small compared to D
[Born and Wolf 1980, cf.]. The characteristic scale of the
Fresnel diffraction effect (that is, roughly speaking, the broadening of the
object shadow) is the so-called Fresnel scale
and small compared to D
[Born and Wolf 1980, cf.]. The characteristic scale of the
Fresnel diffraction effect (that is, roughly speaking, the broadening of the
object shadow) is the so-called Fresnel scale
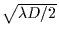 . The
Fresnel scale at 40 AU, observed at
. The
Fresnel scale at 40 AU, observed at
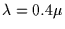 m, is 1.1
km, i.e. a KBO typical size, and so the diffraction must be seriously
taken into account to analyze the occultations by KBOs.
m, is 1.1
km, i.e. a KBO typical size, and so the diffraction must be seriously
taken into account to analyze the occultations by KBOs.
Let us now consider the case of a monochromatic point source occulted
by an opaque spherical object of radius 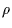 . If
. If 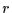 denotes the distance
between the line of sight (the star's direction) and the center of the
object, and if the lengths
denotes the distance
between the line of sight (the star's direction) and the center of the
object, and if the lengths 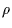 and
and 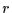 are expressed in the Fresnel scale
unit (noted Fsu hereinafter), the normalized
light intensity
are expressed in the Fresnel scale
unit (noted Fsu hereinafter), the normalized
light intensity 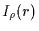 is given by (see appendix B of [Roques, Moncuquet and Sicardy 1987])
is given by (see appendix B of [Roques, Moncuquet and Sicardy 1987])
Outside the geometric shadow (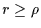 ) :
) :
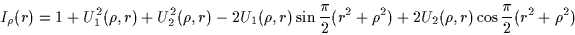 |
(9) |
Inside the geometric shadow (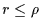 ) :
) :
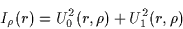 |
(10) |
where 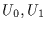 and
and 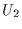 are the Lommel functions defined by (for
are the Lommel functions defined by (for 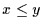 )
)
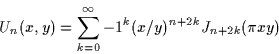 |
(11) |
where 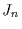 is the Bessel function of order n.
is the Bessel function of order n.
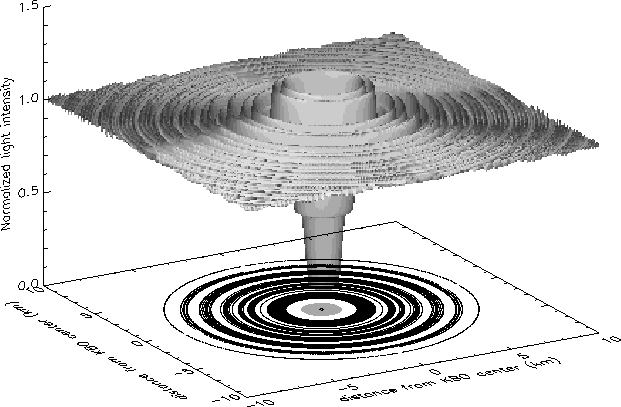
Fig.1(top) shows the diffraction pattern of a circular object (1km
radius) occulting a
point star and is computed using Eq.9 and Eq.10. The
Fresnel scale is set to 1km.
The size of the shadow is larger (about one Fresnel scale)
than the geometric shadow,
and overall the diffraction fringes are visible at a large distance
from the object
(as long as the photometric sensitivity is good).
Figure 1:
The shadow pattern of a 1 km radius KBO in front of a point star.
The two horizontal axis are distances in kilometers and the vertical axis is
the normalized stellar flux. Top:The KBO is circular. Bottom :
The KBO is irregular (the limb is  corrugated) and elliptical
(the eccentricity is 0.7 and the half major axis is 4/3 km,
such that
corrugated) and elliptical
(the eccentricity is 0.7 and the half major axis is 4/3 km,
such that 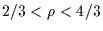 km).
The projected contours show the
km).
The projected contours show the 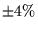 variation of the light
intensity (the black filled areas correspond to
variation of the light
intensity (the black filled areas correspond to 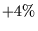 , i.e.
, i.e.  ).
The grey central spot indicates the exact geometric shadow of the
KBO.
).
The grey central spot indicates the exact geometric shadow of the
KBO.
 |



Next: 3.2 Discussion
Up: 3. MODELING A REALISTIC
Previous: 3. MODELING A REALISTIC
DESPA, Observatoire de Paris
2000-04-05
![]() . If
. If ![]() denotes the distance
between the line of sight (the star's direction) and the center of the
object, and if the lengths
denotes the distance
between the line of sight (the star's direction) and the center of the
object, and if the lengths ![]() and
and ![]() are expressed in the Fresnel scale
unit (noted Fsu hereinafter), the normalized
light intensity
are expressed in the Fresnel scale
unit (noted Fsu hereinafter), the normalized
light intensity ![]() is given by (see appendix B of [Roques, Moncuquet and Sicardy 1987])
is given by (see appendix B of [Roques, Moncuquet and Sicardy 1987])
![]() ) :
) :