Let
us take a function that is a sum of two Maxwellian distributions of
densities ![]() and temperatures
and temperatures ![]() , corresponding to the
core (cold) and halo (hot). With such a distribution, one can define
the traditional temperature as
, corresponding to the
core (cold) and halo (hot). With such a distribution, one can define
the traditional temperature as
![]() and the effective temperature as
and the effective temperature as
![]() . For simplicity, we will
write
. For simplicity, we will
write
![]() and
and
![]() (which implies
(which implies
![]() and
and ![]() ). In this case
velocity filtration is especially simple to visualize since
the density of the cold electrons
). In this case
velocity filtration is especially simple to visualize since
the density of the cold electrons ![]() at the
equator is multiplied by a factor
at the
equator is multiplied by a factor
![]() at a
distance
at a
distance ![]() and similarly for hot electrons. One obtains the variation in temperatures with latitude
for such a core + halo distribution to be:
and similarly for hot electrons. One obtains the variation in temperatures with latitude
for such a core + halo distribution to be:
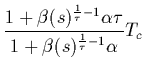 |
(6) | ||
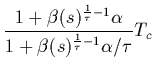 |
(7) |
For Voyager 1, at the distance of
![]() , we have
, we have
![]() and
and
![]() , and if the conditions were
the same for both Voyager 1 and Ulysses, the above equations allow us
to predict that a factor of 4 variation in density should have
produced a 50% variation in
, and if the conditions were
the same for both Voyager 1 and Ulysses, the above equations allow us
to predict that a factor of 4 variation in density should have
produced a 50% variation in ![]() and a 5% variation in
and a 5% variation in ![]() . In
reality, Ulysses measured a doubling of effective temperature for a
factor 4 drop in
. In
reality, Ulysses measured a doubling of effective temperature for a
factor 4 drop in ![]() . The variation in
. The variation in
![]() is very small for a core + halo distribution because
is very small for a core + halo distribution because
![]() is close
to
is close
to ![]() which is constant along a field line since the core is Maxwellian.
which is constant along a field line since the core is Maxwellian.