

Next: 2.3 Maxwellian Core and
Up: 2. Latitudinal Distribution of
Previous: 2.1 Velocity Filtration
Let us first consider the simple case treated by
Meyer-Vernet, Moncuquet and Hoang [1995],
which we will generalize in this paper, of
the following (normalized) 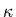 -distribution
-distribution
![$\displaystyle f_{0}\left( v
\right) = \frac{\Gamma(\kappa
+1)}{\pi^{3/2}\kappa^...
...Theta^3} \left[ 1+\frac{v^{2}}{\kappa \Theta^{2}}
\right]^{-\kappa -1}
\protect$](img56.gif) |
|
|
(3) |
where 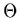 is the most probable speed, which we will
denote the ``thermal-kappa speed'',
in an analogy to the thermal speed of a Maxwellian.
Kappa distributions have been widely used to model space plasmas
[ Vasyliunas, 1968, Collier and Hamilton, 1995] and approximate a Maxwellian at low energies with
a power-law tail at higher energies (a non-thermal halo). Note that
typically kappa distributions are found to have a
is the most probable speed, which we will
denote the ``thermal-kappa speed'',
in an analogy to the thermal speed of a Maxwellian.
Kappa distributions have been widely used to model space plasmas
[ Vasyliunas, 1968, Collier and Hamilton, 1995] and approximate a Maxwellian at low energies with
a power-law tail at higher energies (a non-thermal halo). Note that
typically kappa distributions are found to have a 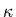 index
between 2 and 6 and that the distribution tends towards a Maxwellian
when
index
between 2 and 6 and that the distribution tends towards a Maxwellian
when
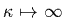 .
In this limit the two temperatures,
.
In this limit the two temperatures,  and
and
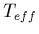 , are equal but for finite
, are equal but for finite 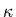 they have the
different values
they have the
different values
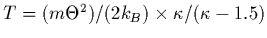 and
and
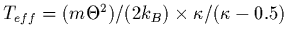 ,
though they both increase with latitude
and obey the same polytropic law. To calculate
the variation of these temperatures with position
,
though they both increase with latitude
and obey the same polytropic law. To calculate
the variation of these temperatures with position  along
the magnetic field line, one inserts (3) in (1) and finds
that the distribution remains a kappa function (with the same
along
the magnetic field line, one inserts (3) in (1) and finds
that the distribution remains a kappa function (with the same
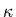 ). Using moments calculation, one finds the density and temperature
profiles to be:
). Using moments calculation, one finds the density and temperature
profiles to be:
![$\displaystyle \frac{n(s)}{n(0)} = {\left[ 1+\frac{2\Phi(s)}{m \kappa \Theta^2} \right]}
^{\frac{1}{2} - \kappa} \protect$](img62.gif) |
|
|
(4) |
![$\displaystyle \frac{T(s)}{T(0)} = \frac{T_{eff}(s)}{T_{eff}(0)} =
\left[\frac{n(s)}{n(0)}\right]
^{\frac{-1}{\kappa - 1/2}}$](img63.gif) |
|
|
(5) |
Thus, with such a 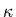 -distribution,
the density and temperature follow a polytropic equation
of state
-distribution,
the density and temperature follow a polytropic equation
of state
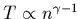 , where the
polytropic index is less than one and related to
, where the
polytropic index is less than one and related to 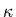 via
via
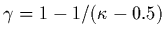 [ Meyer-Vernet, Moncuquet and Hoang, 1995].
[ Meyer-Vernet, Moncuquet and Hoang, 1995].
The
polytropic law (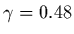 ) observed in the IPT suggests that we should
model the electrons in the torus with a
) observed in the IPT suggests that we should
model the electrons in the torus with a 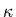 -distribution of
-distribution of
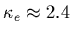 . The measurements do not tell us however
that the ``true'' electron velocity distribution is necessarily a kappa.
Moreover, the
value that we derive for the polytropic law comes from measurements
made along the specific magnetic field line sampled by Ulysses (about
. The measurements do not tell us however
that the ``true'' electron velocity distribution is necessarily a kappa.
Moreover, the
value that we derive for the polytropic law comes from measurements
made along the specific magnetic field line sampled by Ulysses (about
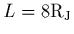 ). The distribution on neighboring field lines does not
necessarily have the same value of kappa or even maintain a kappa-like
distribution.
). The distribution on neighboring field lines does not
necessarily have the same value of kappa or even maintain a kappa-like
distribution.


Next: 2.3 Maxwellian Core and
Up: 2. Latitudinal Distribution of
Previous: 2.1 Velocity Filtration
Michel Moncuquet
DESPA, Observatoire de Paris
2001-08-28
![$\displaystyle f_{0}\left( v
\right) = \frac{\Gamma(\kappa
+1)}{\pi^{3/2}\kappa^...
...Theta^3} \left[ 1+\frac{v^{2}}{\kappa \Theta^{2}}
\right]^{-\kappa -1}
\protect$](img56.gif)
![]() ) observed in the IPT suggests that we should
model the electrons in the torus with a
) observed in the IPT suggests that we should
model the electrons in the torus with a ![]() -distribution of
-distribution of
![]() . The measurements do not tell us however
that the ``true'' electron velocity distribution is necessarily a kappa.
Moreover, the
value that we derive for the polytropic law comes from measurements
made along the specific magnetic field line sampled by Ulysses (about
. The measurements do not tell us however
that the ``true'' electron velocity distribution is necessarily a kappa.
Moreover, the
value that we derive for the polytropic law comes from measurements
made along the specific magnetic field line sampled by Ulysses (about
![]() ). The distribution on neighboring field lines does not
necessarily have the same value of kappa or even maintain a kappa-like
distribution.
). The distribution on neighboring field lines does not
necessarily have the same value of kappa or even maintain a kappa-like
distribution.