« Dis-moi, la lune,
T'habites un coin qu'on n'voit pas bien,
mêm' quand on met nos grosses lunettes... »
Léo Ferré
La magnétosphère jovienne interne est peuplée de particules
chargées, en corotation partielle avec Jupiter et soumises au puissant
champ magnétique de cette planète, formant en particulier entre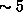 
et 10
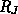(rayon jovien) un nuage de plasma à peu près toroïdal
qu'il est convenu d'appeler le tore de plasma d'Io.
Détecté depuis la terre dès 1976 grâce à des observations de raies
d'émission d'ions soufre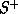 
[Kupo et al., 1976], mais observé
in situ pour la première fois 
en 1979 par la sonde spatiale Voyager 1, ce
plasma est en effet principalement produit par le satellite Io, bien que les
mécanismes physiques à l'oeuvre pour arracher cette matière de l'atmosphère
volcanique d'Io, pour l'ioniser et la transporter de part et d'autre de
l'orbite d'Io (à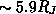 
) sous le «contrôle» du champ magnétique de
Jupiter, soient encore très mal compris. Une première raison à cela tient
naturellement à la difficulté d'appréhender un phénomène qui met en jeu une si
grande variété de processus physico-chimiques, à la frontière de l'aéronomie et
de la physique des plasmas. Une autre raison est la rareté des mesures in situ
(3 passages de sondes depuis Voyager 1 à quelques années d'intervalle)
avec pour principale conséquence un manque de contrainte sur les hypothèses
généralement avancées pour expliquer la structure physico-chimique et la
stabilité (ou non) du tore. Quant aux observations faites depuis la Terre,
elles ont plutôt ajouté à la complexité du phénomène en mettant par exemple en
évidence des dissymétries azimutales persistantes [Schneider and Trauger, 1995, par ex.
,] (autrement dit le tore n'est pas tout à fait un tore de
révolution) ainsi que des variations temporelles [Thomas, 1993, revues
dans,] à moyen ou long terme, que les sondes ne pouvaient évidemment
pas révéler.
Quoi qu'il en soit, le tore de plasma d'Io existe, on l'a rencontré à
plusieurs reprises , en particulier la sonde spatiale européenne
Ulysse, le 8 février 1992. Cette rencontre entre Ulysse et Jupiter fut le point
de départ de cette thèse qui a deux objectifs :
1) Extraire le plus d'informations possible des
observations faites par Ulysse lors de son passage au plus près de Jupiter
( 
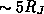). Rappelons qu'Ulysse est une sonde d'exploration solaire
hors-Écliptique, ce qui a eu en l'occurrence deux conséquences, bonne et
mauvaise : la mauvaise est que les instruments d'Ulysse ne sont pas
bien adaptés à la mesure dans la magnétosphère jovienne et qu'il a vraiment fallu
s'acharner sur les observations disponibles pour en tirer des paramètres
physiques. La bonne
conséquence, qui justifiait que l'on s'acharnât, est que la traversée du tore
d'Io s'est accomplie sur une orbite exceptionnelle
, quasiment nord-sud et a fourni pour la première fois et
probablement pour longtemps la seule «coupe» méridienne du tore de
plasma d'Io.
2)
Déterminer si une «certaine» structure spatiale a perduré entre les
observations in situ du tore, et dans ce cas, construire un modèle de
structure 3-D du tore bien étayé physiquement et «fédérateur» de ces
différentes mesures.
Cette approche doit permettre d'une part de comprendre la physique de base qui
détermine l'organisation du tore dans la magnétosphère jovienne
et d'autre part de distinguer dans ce tore de plasma
ce qui est temporellement stable de ce qui est vraisemblablement lié aux
variations météorologiques (au sens le plus large) d'Io et de Jupiter.
Ajoutons qu'au delà de la légitime ambition de comprendre «comment ça
marche», il est aussi nécessaire de modéliser le tore de plasma d'Io en 3
dimensions pour pouvoir étudier et interpréter les émissions radio de Jupiter
observées depuis la Terre, dont on sait qu'elles sont contrôlées et/ou
produites par ce tore de plasma [Kaiser, 1993, par ex.,].
Le premier objectif - l'exploitation des observations d'Ulysse -
m'a donné du fil à retordre mais a été plus qu'atteint : on a pu déduire des
spectres radio les densités et surtout les températures des électrons avec
des précisions de 15 à 20%, précisions suffisantes pour établir que les
températures électroniques variaient fortement avec la latitude, ce
qui constitue une véritable découverte. En effet, jusqu'au passage d'Ulysse
près de Jupiter, la plupart des connaissances quantitatives de la structure
spatiale du tore d'Io (densités et températures) provenaient des mesures faites
par Voyager 1. Or cette sonde est restée à peu près dans le plan équatorial du
tore, de sorte que, dans les modèles à deux dimensions, seule la structure
radiale reposait sur des mesures in situ, tandis que la structure latitudinale
était calculée à partir d'hypothèses plausibles mais non vérifiées
expérimentalement. Ces modèles de densité [Bagenal and Sullivan, 1981, Divine and Garrett, 1983, Bagenal, 1994] ont
été largement utilisés pour préparer la visite de la sonde Galileo qui, comme
Voyager, ne s'est guère éloignée de l'équateur. En revanche Ulysse a traversé
le tore d'Io le long d'une trajectoire presque nord-sud et a exploré plusieurs
échelles de hauteur de part et d'autre de l'équateur du tore, tout en restant
sur les 2/3 de sa trajectoire à peu près sur une même coquille magnétique (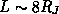 
). La variation significative de la température des électrons le long
de cette trajectoire contredit l'hypothèse, fondatrice de tous les modèles
précédents, de l'équilibre thermique du plasma
(espèce par espèce) le long des lignes de force
magnétiques et infirme le modèle de confinement équatorial des particules qui en
découlait.
Après cette découverte, le deuxième objectif annoncé de la thèse - comprendre et modéliser le tore spatialement - a été réduit (d'au moins une dimension) et surtout, l'approche de cet objectif a changé. En effet, notre intention première (c'est-à-dire avant l'obtention de la température électronique) était d'utiliser les densités vues par Ulysse pour donner une échelle de hauteur gaussienne de la variation densité/latitude, dans le cadre d'un modèle classique fondé sur l'équilibre diffusif du plasma le long des lignes de champ (ce qu'on a fait dans [Hoang et al., 1993]) et de se concentrer, pour construire un modèle de densité, sur la compréhension du mécanisme de diffusion radiale du plasma et éventuellement l'analyse des dissymétries de révolution. Mais l'hypothèse d'équilibre thermique local (qui implique une température constante le long des lignes de champ) s'avérant fausse, ce scénario a changé : il a fallu d'une part expliquer les résultats inattendus d'Ulysse et d'autre part proposer un nouveau modèle de structure latitudinale (ou confinement) du tore qui tienne compte de ces résultats. C'est finalement ce travail d'explication théorique et de modélisation du confinement du tore qui va constituer l'essentiel de la deuxième partie de cette thèse. Pour la structure radiale, on se contentera comme dans [Bagenal, 1994] d'une description empirique (fondé sur des profils de densité mesurés et supposés indépendant de la longitude) sans chercher à expliquer les mécanismes physiques qui font diffuser le plasma radialement. Néanmoins, notre nouveau modèle permettra, comme c'était notre ambition, d'expliquer et fédérer plusieurs mesures in situ et ainsi d'apprécier la stabilité temporelle du tore de plasma d'Io.
Pour expliquer la variation observée de la température électronique, qui
augmente avec la latitude et est anticorrélée à la densité, nous invoquons un
mécanisme dit de «filtrage des vitesses», proposé par [Scudder, 1992a]&b dans
un tout autre contexte. Ce mécanisme est à l'oeuvre dès lors que le
plasma étudié est à la fois soumis à une force dérivant d'un potentiel
attractif (ici la force centrifuge due à la corotation), et n'est pas à
l'équilibre thermique de Maxwell-Boltzmann. On peut en donner l'explication
préliminaire suivante :
les particules sont confinées dans le puits de potentiel (qui définit ici
l'équateur centrifuge) et puisque les particules les plus énergétiques
s'échappent plus facilement, leur proportion est plus grande en dehors du puits
de potentiel, et donc l'énergie cinétique moyenne des particules augmente avec
la latitude centrifuge tandis que la densité diminue. Ce filtrage des vitesses
n'a pas lieu avec une distribution maxwellienne des vitesses parce que dans ce
cas le potentiel «filtre» toutes les particules de la même façon
. Ce mécanisme de filtrage des vitesses fait ici
merveille pour expliquer les mesures des densités et températures électroniques
obtenues sur la trajectoire quasiment nord-sud d'Ulysse [Meyer-Vernet, Moncuquet and Hoang, 1995].
Pour obtenir un modèle quantitatif, on a utilisé une distribution d'énergies
empirique, fréquemment rencontrée dans les plasmas naturels
[Olbert et al., 1968], appelée distribution lorentzienne généralisée ou
distribution «kappa» (notée encore 
-distribution), et qui permet de
décrire simplement et de manière réaliste un plasma stable hors équilibre
thermique.
Ainsi, l'augmentation des températures le long des lignes de champ
est incompatible avec l'équilibre thermique local des électrons, mais peut en
revanche s'expliquer par la permanence d'une population d'électrons
suprathermiques dont les énergies décroissent en loi de puissance comme dans
une -distribution. La permanence d'une telle population est compatible
avec le fait que le plasma du tore est très peu collisionnel et n'a
effectivement pas beaucoup de raisons de relaxer rapidement vers l'équilibre
thermique.
Ces résultats d'Ulysse ne concernent malheureusement que les électrons,
alors que l'organisation spatiale du tore dans le potentiel centrifuge est
principalement contrôlée par les ions qui sont beaucoup plus massifs. Néanmoins, l'argument
d'absence d'équilibre qui vaut pour la
distribution des électrons doit valoir a priori pour les ions : leur libre
parcours moyen est environ 6 fois plus grand que celui des électrons et on
s'attend donc encore moins à ce qu'ils thermalisent. Bien entendu, leurs
distributions d'énergies initiales peuvent être très complexes, car elles sont
liées au mécanisme de pick-up
(ou d'assimilation) des neutres ( qui sont
«brutalement» ionisés dans leur mouvement keplerien autour de Jupiter et
les ions ainsi formés se retrouvent prisonniers des lignes de champ, en
corotation avec Jupiter). On trouve dans la littérature un choix abondant
de ces distributions de pick-up mais aucune n'a été vérifiée expérimentalement.
Quoi qu'il en soit, le mouvement des ions assimilés est déterminé par l'action
du fort champ magnétique de Jupiter et va se caractériser par un comportement
certes très différencié entre les particules évoluant parallèlement ou
perpendiculairement au champ, c'est-à-dire anisotrope, mais qui va
relaxer dans chaque direction (sinon tendre vers l'équilibre thermique)
lorsqu'on «s'éloigne» (en espace et en temps) du lieu d'assimilation
des neutres.
Le modèle de structure (en densité et température) que nous
proposons ici sera donc construit par analogie avec ce que nous observons pour
les électrons, c'est-à-dire à l'aide de distributions kappa mais en y ajoutant
la possibilité d'une (forte) anisotropie de température, puisqu'elle est
soupçonnée d'être importante pour les ions, à cause du mécanisme
d'assimilation des neutres dans un plasma en corotation (esquissé ci-dessus).
Cela m'a naturellement
conduit à utiliser des distributions kappa dans deux directions, parallèle et
perpendiculaire au champ magnétique (que nous appellerons «bi-kappa»), pour
modéliser les différentes populations d'ions. À cet égard ce modèle repose
comme les précédents sur des hypothèses plausibles mais non vérifiées
expérimentalement - moins une cependant,
celle de la température supposée constante avec la latitude -
en particulier à cause de la méconnaissance des «vraies»
distributions d'énergies des ions (une façon de remédier à cela serait par
exemple de «revisiter» les données des analyseurs de particules de Voyager
1 en ajustant ces distributions bi-kappa, ce qui est hors du cadre de cette
thèse, mais est en cours).
La résolution du système d'équations, obtenu en décrivant le plasma du
tore à l'aide de ces distributions bi-kappa anisotropes, n'aboutit qu'à donner
la variation des densités en fonction de la latitude (avec cependant en prime,
par rapport aux modèles isothermes, la variation des températures le long des
lignes de champ). Il faut encore, pour obtenir un modèle digne de ce nom, soit
bâtir un modèle théorique de diffusion radiale
(je mentionne cela pour mémoire,
car je n'aborderai pas cette possibilité qui constitue en soi un vaste et
difficile sujet [Ferrière and Blanc, 1996, par ex.,]),
soit se donner
empiriquement un profil radial de densité à partir des mesures disponibles,
c'est-à-dire pour le moment celles de Voyager 1, et bientôt, je l'espère,
celles de Galileo.
Avec un choix arbitraire des kappa des ions et des anisotropies, en se dotant de
plus d'un bon modèle de champ magnétique , on obtient
finalement un modèle 2-D des densités et des températures pour chacune des
espèces de particules détectées dans le tore.
Une vérification de la validité d'un tel modèle consiste à tester sa
capacité de prédiction pour quelques mesures in situ (autres que celles qui ont
servi de base empirique au modèle, évidemment !). On verra que des mesures
obtenues par trois des
quatre sondes qui ont visité le tore (ou sa banlieue) peuvent être
expliquées à la lumière de ce nouveau modèle. Notamment, on montre que
l'augmentation importante de la température des ions mesurée par Voyager 1 à
partir d'environ 9 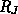, inexpliquée jusqu'à maintenant, pourrait bien être
due à l'élévation en latitude de la sonde à cette distance et donc à un effet
de filtrage des vitesses «vu» le long de sa trajectoire. On montre aussi
que la densité électronique, relativement élevée, mesurée par Ulysse assez loin
du tore (au delà de l'orbite d'Europe et à quelque 20° de latitude
centrifuge) est correctement prédite par notre modèle, ainsi d'ailleurs que
celle mesurée à des distances et latitudes comparables par Voyager 2.
Enfin, si Galileo a mesuré des densités électroniques étonnamment élevées
près de l'orbite d'Io et difficiles à interpréter pour le moment, on peut
constater qu'en s'éloignant de ce lieu «tourmenté», les électrons sont
globalement plus confinés près de l'équateur et moins raréfiés que prévu aux
plus hautes latitudes [Gurnett et al., 1996, par ex.,]; on verra
dans cette thèse
que notre nouveau modèle modifie les prédictions de
densité des modèles précédents dans ce sens.
Tel qu'il se présente à la fin de cette thèse, ce modèle
n'est prédictif que dans une seule
dimension, celle de l'extension du tore en latitude, et reste empirique pour
l'extension radiale (fondé sur les données de Voyager 1, et supposé symétrique
azimutalement). Mais il remet en cause ce qui était considéré à tort avant
Ulysse comme la structure la mieux comprise du tore de plasma d'Io, à savoir
son confinement de part et d'autre de l'équateur centrifuge.
Il constitue aussi pour les radio-astronomes jovitropes une amélioration des modèles empiriques
existants en donnant une vue plus réaliste de l'extension latitudinale du tore.