This simple model can thus explain the polytrope
law of index 
found in Section 3,
if the electron
velocity distribution can be approximated by a Kappa function of the form
(10) with
This function is shown in Fig.3 and compared to its
Maxwellian limit given in (11). Both distributions are
rather similar for 
, i.e. at energies of
the order
or smaller than 
, whereas the Kappa function exhibits
a
supra-thermal tail at higher energies. Note that Eqs.(12)-(
13) yield 
with this value of
. Since measured velocity distributions are often represented
as
the superposition of a cold and a hot
Maxwellian, we compare in Fig.4 the above Kappa function with
a sum of two Maxwellians having parameters of the order of those
inferred from Voyager analysers in the range of Jovicentric
distances explored here
([Sittler and Strobel 1987], [Bagenal 1994]).
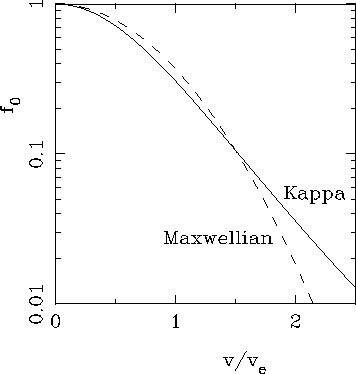
Figure 3: Kappa distribution defined
in Eq.(10) with given in (19), compared to its
Maxwellian limit (11).
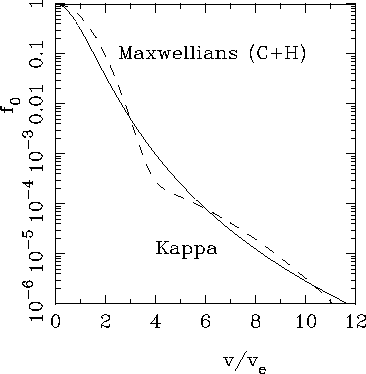
Figure 4: Kappa distribution defined in Eq.(10) with given in (19), compared to a distribution made of the sum of two
Maxwellians (C,H) of densities and temperatures such that 
, 
(for this comparison, the cold temperature has been
arbitrarily chosen equal to 
).
In practice, the electron velocity
distribution is not a priori expected to fit exactly such a
Kappa function. Then, one will not find an exact polytrope law,
but the density and temperature will still be anticorrelated
along field lines, and mimic an approximate polytrope with 
.
For example, the distribution made of a sum of two Maxwellians
also results in a temperature increase with latitude; this can
be easily understood: while the temperature of each Maxwellian
does not change with z, the proportion of the hot component
increases because it is less confined by the potential. However,
with such a cold-plus-hot distribution having parameters of the
order of those inferred from Voyager analysers (Fig.4), the
temperature increase is rather small: Eq.(1) shows that
a
four-fold decrease in cold density (for example) produces an increase
in
by only 5% (instead of the factor of two observed here and
explained by the Kappa distribution of Fig.4). Note also that
the magnetic force, which should modify the above result since
it does not derive from a conservative potential, is not
expected to destroy the anticorrelation between density and
temperature so long as the magnetic field variation is small
over a characteristic scale length.
