5.2 Implementation using high speed photometry

High speed photometric observations of stars have been developed to study rapidly evolving phenomena such as occultation by solar system objects or asteroseismology. A complete analysis of the perturbations in a high speed photometric lightcurve and in occultation lightcurves in particular can be found in [Warner 1988]. If the star is not too faint, the noise on a high time resolution lightcurve is dominated by scintillation which affects the stars independent of their brightness. The r.m.s. signal fluctuation observed with a telescope with a d diameter, at an altitude $h$ above the sea level can be written as [Young 1967]:

$$\sigma = S_0 d^{-2/3} X^{3/2} e^{h/H_0}(2 \tau)^{-1/2}$$ (15)

where $X$ is the airmass, $\tau$ is the integration time, $H_0$ is taken to be 8 km. $S_0$ is a constant equal to $0.09$ for conditions of good seeing, d is in centimeters and $\tau$ is in seconds.

For $\tau=1$ second, the r.m.s. fluctuations on a 2.-m class telescope is roughly $310^{-3}$ for optimal conditions. According to Table I, this will allow us to detect (at $4\sigma$) sub-kilometer objects. The largest ground-based telescopes (i.e. the 10-meters class telescopes) allow us to marginally reach $\sigma \approx 10^{-3}$ and then to detect about 40m radius KBOs (see Table I).

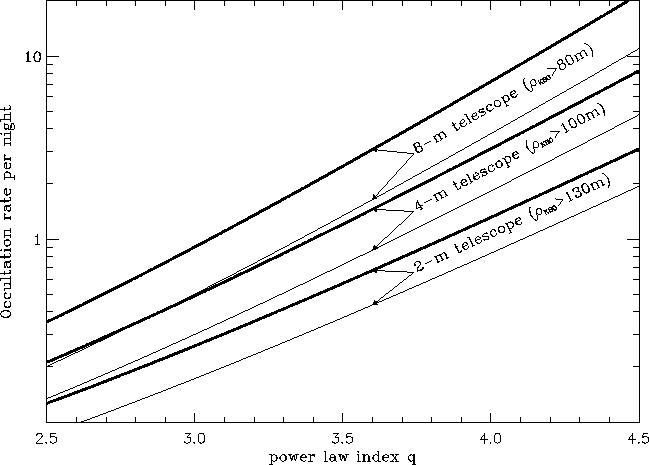
Some useful results, concerning the 2.-, 4.- and 8.-m class telescopes when observing O5 class stars for two magnitudes (12 or 10), are summarized on Fig.4, where we have plotted the occultation rates per night as a function of the power law index q of the sub-kilometer KBO size distribution (with $q = 4$ for $\rho > 1$km as in Table II). We have also indicated on this figure, for each telescope diameter, the approximate radius of the smallest KBO detectable with the considered telescope. In each case, $N_{\rm {occ}}$ is computed for optimum observing conditions, i.e. O5 stars, observed from good sites, in the ecliptic and at the opposition, with telescopes equipped with a sufficiently rapid photometer (at least 20Hz). Figure 4 shows that $N_{\rm {occ}}$ increases exponentially with q but this variation also strongly depends on observational circumstances: We may thus expect that an observation campaign on various sites and/or with different instruments and/or observing different stars could provide by cross-checking a good estimation of q concerning these elusive small KBOs. One can also see on Fig.4 how much the choice of the star is important for implementing the search for occultations by KBOs: For example, the decrease in occultation rate is roughly the same when passing from a 8-m to a 4-m telescope with an O5 star of 12th magnitude as when passing from a 12th to the 10th magnitude O5 star with a 8-m telescope.

Figure 4: Occultation rate per night as a function of the power law index q of the KBOs size distribution, for 2-, 4- and 8-m telescopes, equipped with a 20Hz photometer when observing an O5 star (in optimal conditions) of visual magnitude 12 (bold lines) or magnitude 10 (thin lines).

Let us finally remark that, in the tables I and II, the $\sigma = 5~10^{-4}$ case is unreachable from the ground, but might be achievable in space, if we get fast enough photometry on such space facilities (present or future). In this case, the number of occultations could be indeed spectacular and decisive for our knowledge of the Kuiper belt size distribution.