


Next: 3. MODELING A REALISTIC
Up: A Detection Method for
Previous: 1. INTRODUCTION
2. THE STATISTICAL RATE OF STELLAR OCCULTATION BY KBOs:
A
FIRST APPROACH
The occultation statistical rate is the probable number of occultations of a star
detected during a given time interval. When an observer (on the Earth in most
cases) crosses the shadow of a KBO cast by a star, the star light is not fully
extinguished and the stellar flux oscillates: If these oscillations are
detected, there is an occultation, and the whole region where these
oscillations can be detected is called the diffraction shadow. So, the
occultation rate is computed as the probability of intersection in the sky
plane of the star disc with the KBOs diffraction shadows.
If, at first, we ignore diffraction, the definition of an
occultation event simplifies: there is an occultation when the
observer crosses the geometric shadow of a KBO, and the star light is fully or
partially extinguished, depending only on geometric parameters linked to the
KBO and to the star. In addition, the detection of an
occultation event depends on the conditions of the observation and in particular on
the instrument used for recording the occultation. In the following discussion,
we estimate this ``geometric'' occultation rate by KBOs for a given
star; we defer the possibility of modeling
and exploiting the diffraction phenomenon to later sections.
We consider a population of KBOs moving with respect to a star
in the sky plane. There is an occultation of the star by a KBO if the minimum
distance between the two objects is smaller than the sum of their radii.
We may then write the number of geometric occultations of a star with
angular radius 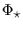 and with an inclination i on the
Ecliptic plane, by KBOs of angular radius between
and with an inclination i on the
Ecliptic plane, by KBOs of angular radius between
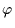 and
and
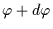 ,
observed during an interval
,
observed during an interval 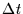 as:
as:
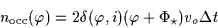 |
(1) |
where
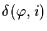 is the density of KBOs in the sky plane
and
is the density of KBOs in the sky plane
and 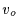 is the KBOs velocity in the sky plane.
is the KBOs velocity in the sky plane.
The total number of occultations during 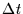 is then:
is then:
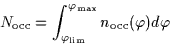 |
(2) |
where
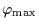 is the maximum expected angular radius of KBOs (this
value is not critical since we know that big KBOs are very rare, i.e.
is the maximum expected angular radius of KBOs (this
value is not critical since we know that big KBOs are very rare, i.e.
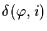 must be
vanishingly small for large
must be
vanishingly small for large 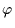 ) and
) and
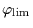 is the angular radius of the smallest KBO detectable by
occultation.
is the angular radius of the smallest KBO detectable by
occultation.
Let us now discuss the three main parameters governing this geometric
occultation rate, which are:
- The density of the KBOs which is
poorly known: The high
magnitude of these objects limits the size of the directly detectable objects
to few kilometers, but we assume that the Kuiper Belt has a
size distribution
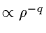 with a constant index q
extending to meter-sized objects.
The Near Earth Asteroid (NEA) population (the only small body population in the
Solar system known down to meter-sized objects) indeed has a size distribution with
an index more or less constant to 5m radius [Rabinowitz et al. 1994]. We will return to the assumption of a constant index q
in section 4.
In addition, the KBOs are assumed to follow an
exponential distribution in inclination with an angular scale height H and the
spatial density of KBOs is also assumed to depend on the distance to the
sun, D , with the same law as the protoplanetary disk, i.e. as
with a constant index q
extending to meter-sized objects.
The Near Earth Asteroid (NEA) population (the only small body population in the
Solar system known down to meter-sized objects) indeed has a size distribution with
an index more or less constant to 5m radius [Rabinowitz et al. 1994]. We will return to the assumption of a constant index q
in section 4.
In addition, the KBOs are assumed to follow an
exponential distribution in inclination with an angular scale height H and the
spatial density of KBOs is also assumed to depend on the distance to the
sun, D , with the same law as the protoplanetary disk, i.e. as 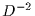 .
If we assume N KBOs larger than 1km exist,
located between 30 and
.
If we assume N KBOs larger than 1km exist,
located between 30 and 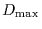 AU, the previous
assumptions lead to the following 2-D differential size distribution
AU, the previous
assumptions lead to the following 2-D differential size distribution
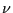 , which is the number of KBOs of radius between
, which is the number of KBOs of radius between 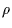 (in km)
and
(in km)
and 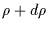 , with inclination between i (in degrees) and
, with inclination between i (in degrees) and 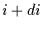 ,
and at an heliocentric distance between D (in AU and >30 AU) and
,
and at an heliocentric distance between D (in AU and >30 AU) and 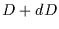 :
:
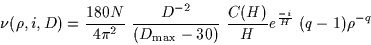 |
(3) |
with
![$C(H)= \frac{\pi[(180/\pi)^{2} + H^{2}]}{180[180/\pi + H
e^{-90/H}]} \simeq 1+\sin^{2}H$](img56.gif) ,
where H is expressed in degrees, and
,
where H is expressed in degrees, and 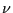 is
given per AU and per steradian.
is
given per AU and per steradian.
Recent observations allow us to estimate 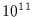 objects
larger than 1 km, located between 30 and 50 AU (the practical limit of
existing surveys), a differential size distribution index
objects
larger than 1 km, located between 30 and 50 AU (the practical limit of
existing surveys), a differential size distribution index 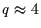 and a latitudinal scale height
and a latitudinal scale height
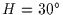 [Jewitt 1999].
Then, by substituting these values in Eq.3 and by integrating in D
between 30 and 50 AU, we obtain the
following mean density of KBOs in the sky plane of angular radius between
[Jewitt 1999].
Then, by substituting these values in Eq.3 and by integrating in D
between 30 and 50 AU, we obtain the
following mean density of KBOs in the sky plane of angular radius between
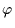 and
and
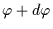 and with inclination between i and
and with inclination between i and 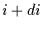 :
:
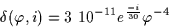 |
(4) |
where, for convenience,
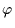 is expressed in mas(=
is expressed in mas(=
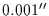 )
and
)
and 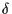 is so given per
is so given per 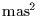 .
Let us note that, if we assume the KBOs size distribution ranges from
one meter to some hundreds of kilometers
(that is from about
.
Let us note that, if we assume the KBOs size distribution ranges from
one meter to some hundreds of kilometers
(that is from about 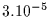 to
to 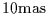 at 40 AU), we can estimate
an optical depth of the Kuiper Belt in the ecliptic of
at 40 AU), we can estimate
an optical depth of the Kuiper Belt in the ecliptic of
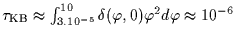 . We
will show however in section 4 that diffraction perturbs the stars light far
away from the geometric disc, so that the proportion of the ecliptic sky
perturbed by the Kuiper Belt is much
larger than that inferred by the optical depth
. We
will show however in section 4 that diffraction perturbs the stars light far
away from the geometric disc, so that the proportion of the ecliptic sky
perturbed by the Kuiper Belt is much
larger than that inferred by the optical depth
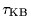 .
.
- The velocity of the KBOs in the sky plane
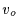 which is involved
in both the number of occultations (
which is involved
in both the number of occultations (
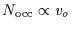 ) and the duration of the
occultation (
) and the duration of the
occultation (
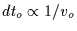 ). It is given as
). It is given as
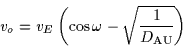 |
(5) |
where 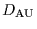 is the heliocentric distance of the KBOs in astronomical
units,
is the heliocentric distance of the KBOs in astronomical
units, 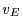 is the Earth's orbital speed,
is the Earth's orbital speed, 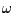 is the
angle between the KBO and the anti-solar direction which is called "opposition"
hereinafter.
is the
angle between the KBO and the anti-solar direction which is called "opposition"
hereinafter.
Because 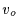 depends on the distance D of the occulting objects, so do the
probability and the duration of the occultations. This property could allow the
discrimination between an occultation by a KBO and an occultation by an
asteroid or a comet (see section 6).
By fixing D to 40 AU and having
depends on the distance D of the occulting objects, so do the
probability and the duration of the occultations. This property could allow the
discrimination between an occultation by a KBO and an occultation by an
asteroid or a comet (see section 6).
By fixing D to 40 AU and having 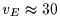 km/s, we get
km/s, we get
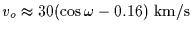 (
(
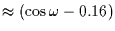 mas/s). Then
mas/s). Then 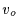 is maximum (
is maximum (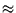 25 km/s)
toward the opposition and decreases toward a direction, called the
"quadrature" hereinafter, for which
25 km/s)
toward the opposition and decreases toward a direction, called the
"quadrature" hereinafter, for which
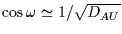 , i.e.
, i.e.
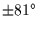 for an object at 40 AU. An occultation, usually very brief,
becomes slower in this direction. For instance, if an occultation by a 1km
radius KBO was detected, it could last from about 0.1 to few seconds, as
for an object at 40 AU. An occultation, usually very brief,
becomes slower in this direction. For instance, if an occultation by a 1km
radius KBO was detected, it could last from about 0.1 to few seconds, as
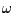 goes from the opposition to the quadrature.
goes from the opposition to the quadrature.
- The size of the smallest KBOs detectable by occultation
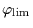 depends on the angular radius of the star
depends on the angular radius of the star 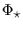 and on that of the KBO
itself: An object which is too small passing in front of the star will not generate a
detectable decrease in the stellar flux. For a KBO smaller than the
stellar disc,
geometrical optics gives the straightforward condition:
and on that of the KBO
itself: An object which is too small passing in front of the star will not generate a
detectable decrease in the stellar flux. For a KBO smaller than the
stellar disc,
geometrical optics gives the straightforward condition:
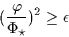 |
(6) |
where 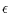 is the detection threshold or sensitivity of the
instrument. This yields for instance a detection threshold
is the detection threshold or sensitivity of the
instrument. This yields for instance a detection threshold
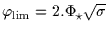 at
at
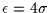 , where
, where
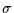 is the r.m.s. signal fluctuations (i.e. the photometric precision
limit of the instrument), and with
is the r.m.s. signal fluctuations (i.e. the photometric precision
limit of the instrument), and with 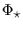 typically about 0.01 to 1 mas. But, as we shall see in subsequent sections,
these formulae are quite approximate and only valid for a large
stellar radius
(>0.1 mas) because diffraction is not taken into
account: the real detection threshold not only depends on the star size in a
very different way than stated here, but also depends on both the distance from
the KBO to the observer and the observation wavelength.
typically about 0.01 to 1 mas. But, as we shall see in subsequent sections,
these formulae are quite approximate and only valid for a large
stellar radius
(>0.1 mas) because diffraction is not taken into
account: the real detection threshold not only depends on the star size in a
very different way than stated here, but also depends on both the distance from
the KBO to the observer and the observation wavelength.
We may finally deduce from Eq.2 and Eq.4 and the discussion above, the
following approximation of the total number of geometric occultations by KBOs
of a star with an angular radius 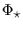 and an inclination i on the Ecliptic:
and an inclination i on the Ecliptic:
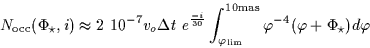 |
(7) |
where 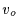 is expressed in mas/s,
is expressed in mas/s, 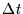 in hours,
in hours,
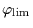 and
and 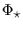 in mas.
For instance,
we may estimate the geometric occultation rate per night (8 hours) in the
Ecliptic for a
in mas.
For instance,
we may estimate the geometric occultation rate per night (8 hours) in the
Ecliptic for a
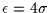 sensitivity, and
sensitivity, and
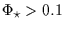 mas as:
mas as:
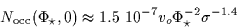 |
(8) |
So this geometric occultation rate per nigh is less than 0.1
in the most favourable case,
with a typical KBO detection threshold of a few kilometers in size.
Fortunately, as we will show in section 4, this result, which does not take
into account any diffraction effects, significantly underestimates
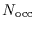 .
.



Next: 3. MODELING A REALISTIC
Up: A Detection Method for
Previous: 1. INTRODUCTION
DESPA, Observatoire de Paris
2000-04-05
![]() and with an inclination i on the
Ecliptic plane, by KBOs of angular radius between
and with an inclination i on the
Ecliptic plane, by KBOs of angular radius between
![]() and
and
![]() ,
observed during an interval
,
observed during an interval ![]() as:
as:
![]() is then:
is then:
![]() objects
larger than 1 km, located between 30 and 50 AU (the practical limit of
existing surveys), a differential size distribution index
objects
larger than 1 km, located between 30 and 50 AU (the practical limit of
existing surveys), a differential size distribution index ![]() and a latitudinal scale height
and a latitudinal scale height
![]() [Jewitt 1999].
Then, by substituting these values in Eq.3 and by integrating in D
between 30 and 50 AU, we obtain the
following mean density of KBOs in the sky plane of angular radius between
[Jewitt 1999].
Then, by substituting these values in Eq.3 and by integrating in D
between 30 and 50 AU, we obtain the
following mean density of KBOs in the sky plane of angular radius between
![]() and
and
![]() and with inclination between i and
and with inclination between i and ![]() :
:
![]() depends on the distance D of the occulting objects, so do the
probability and the duration of the occultations. This property could allow the
discrimination between an occultation by a KBO and an occultation by an
asteroid or a comet (see section 6).
By fixing D to 40 AU and having
depends on the distance D of the occulting objects, so do the
probability and the duration of the occultations. This property could allow the
discrimination between an occultation by a KBO and an occultation by an
asteroid or a comet (see section 6).
By fixing D to 40 AU and having ![]() km/s, we get
km/s, we get
![]() (
(
![]() mas/s). Then
mas/s). Then ![]() is maximum (
is maximum (![]() 25 km/s)
toward the opposition and decreases toward a direction, called the
"quadrature" hereinafter, for which
25 km/s)
toward the opposition and decreases toward a direction, called the
"quadrature" hereinafter, for which
![]() , i.e.
, i.e.
![]() for an object at 40 AU. An occultation, usually very brief,
becomes slower in this direction. For instance, if an occultation by a 1km
radius KBO was detected, it could last from about 0.1 to few seconds, as
for an object at 40 AU. An occultation, usually very brief,
becomes slower in this direction. For instance, if an occultation by a 1km
radius KBO was detected, it could last from about 0.1 to few seconds, as
![]() goes from the opposition to the quadrature.
goes from the opposition to the quadrature.
![]() and an inclination i on the Ecliptic:
and an inclination i on the Ecliptic: