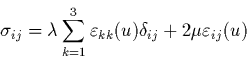

Next: 0.3.3 Problèmes stationnaires
Up: 0.3 Élasticité linéaire
Previous: 0.3.1 Analogie avec la
La théorie de l'élasticité linéaire se situe d'une part dans le cadre
de la description des solides lentement déformables8
esquissée ci-dessus,
et d'autre part on impose que la loi de comportement élastique
reliant le tenseur des contraintes à celui des déformations est
linéaire.
Lorsque de plus le solide élastique a un comportement isotrope
(c'est-à-dire ne privilégie aucune direction de l'espace), on obtient
la loi de comportement de Hooke:
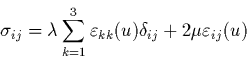 |
(41) |
 et
et  sont les coefficients de Lamé.
Le système linéaire que constitue l'équation (41) s'inverse
facilement:
sont les coefficients de Lamé.
Le système linéaire que constitue l'équation (41) s'inverse
facilement:
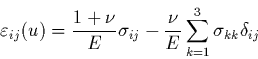 |
(42) |
où on a posé
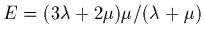 qui est le module
d'Young et
qui est le module
d'Young et
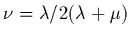 qui est le coefficient de
Poisson.
qui est le coefficient de
Poisson.
Dans la pratique, ce sont les module d'Young et coefficient de
Poisson qui sont connus expérimentalement pour un matériau homogène
donné et on en déduit les coefficients de Lamé :
 |
(43) |
Toujours dans le cas d'un matériau homogène, les différents
coefficients introduits ci-dessus sont des constantes et dans ce cas,
la conservation de la quantité de mouvement (40) s'écrit
vectoriellement:
 |
(44) |
ou sous la forme équivalente
 |
(45) |
On en dira pas davantage9
concernant les problèmes dynamiques
(i.e. dépendant du temps) de
l'élasticité linéaire, si ce n'est qu'on peut deviner au vu de
l'équation (44) qu'ils peuvent mener sous certaines hypothèses
et cas particulier (notamment d'étude des vibrations dans un milieu élastique) à
l' équation modèle des ondes de type (expression formelle où u désigne un champ inconnu scalaire)
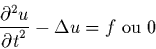 |
(46) |


Next: 0.3.3 Problèmes stationnaires
Up: 0.3 Élasticité linéaire
Previous: 0.3.1 Analogie avec la
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05