- ... comportement1
- On peut
imaginer (et il existe) des lois de comportement plus complexes que
l'éq.(3) pour un fluide : disons simplement que pour décrire les fluides
dits «classiques» ou «newtoniens» considérés ici, les contraintes sont
supposées dépendre linéairement des déformations, ce qui conduit à des
lois de comportement de type (3). Dans tous les autres cas, le
fluide sera dit «non newtonien».
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fluide2
- Des conditions supplémentaires de continuité sont généralement
nécessaires, notamment pour décrire des systèmes comportant plusieurs fluides,
à la traversée d'une surface de contact (séparation entre deux fluides non
miscibles et en particulier, surface libre en contact avec l'atmosphère).
Ces conditions sont relativement simples à énoncer ( par exemple égalité des
vitesses et des
pressions de part et d'autre de la surface de contact), mais il faut
savoir que le problème d'écoulement fluide est alors très sérieusement compliqué
par le fait que la surface de
contact est une inconnue supplémentaire du problème, ce qui nécessite des
traitements analytiques et/ou numériques au cas par cas. C'est pourquoi
nous n'aborderons pas ici ce type de problèmes et nous nous
limiterons au cas ou le volume
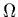 est limité par une paroi
solide ou au cas complémentaire (fluide infini baignant un objet
solide), ou un mélange des deux
est limité par une paroi
solide ou au cas complémentaire (fluide infini baignant un objet
solide), ou un mélange des deux
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vectorielle3
- le terme non-linéaire dans (9) s'écrit aussi:
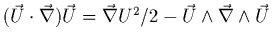
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Stokes4
- ce système nécessite
a priori aussi une condition initiale sur l'état du système à un temps
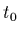 ,
mais comme il est surtout utilisé dans le cas stationnaire,
nous l'avons omise ici
,
mais comme il est surtout utilisé dans le cas stationnaire,
nous l'avons omise ici
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fluides5
-
Ce survol des grandes équations de la mécanique des fluides classique est
empruntée pour l'essentiel au premier chapitre de
Analyse mathématique et calcul
numérique pour les sciences et les techniques, de R. Dautray et J-l
Lions, Ed. Masson, Paris, 1987, qui constitue une véritable
encyclopédie de l'analyse mathématiques des grandes
équations posées en Physique, mais est d'un niveau mathématique très
élevé et à ce titre peu utilisable comme simple
«boite à outil» pour la résolution numérique des équations de
Navier-Stokes par exemple.
On trouvera par contre une description assez complète et très pragmatique
des méthodes numériques
utilisées spécifiquement en mécanique des fluides dans Computational methods for
fluid flow, de R. Peyret et T.D. Taylor, Springer-Verlag, New-York,
1990
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... explicitement6
- Attention, le vecteur accélération des particules n'est pas nul, on a
en effet:
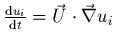
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... d'applications7
- Lorsque
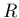 et
et 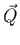 sont
nuls en même temps, l'évolution du milieu est dite adiabatique.
sont
nuls en même temps, l'évolution du milieu est dite adiabatique.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... déformables8
- On suppose
également que les effets mécaniques et
thermiques sont découplés et peuvent être étudiés séparément
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... davantage9
- voir le cours spécifique
d'élasticité linéaire et éléments finis
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
équations10
- ou, de manière équivalente:
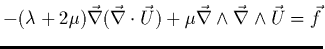
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... champs11
- en fait dans la plupart des
problèmes,
les contraintes et les déplacements ne peuvent être déterminés
indépendamment l'un de l'autre, d'où le succès des «formulations
variationnelles» pour résoudre ces problèmes
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
généralisée12
- brièvement, pour tout tenseur
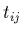 ,
on
,
on
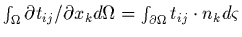
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... régulier13
- disons que
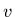 est supposé être une fonction de carré intégrable sur
est supposé être une fonction de carré intégrable sur 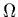
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vous14
- mais que vous utiliserez d'autant mieux que vous avez une
idée précise de ce qu'ils font
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'antenne1.1
- le signal
réel collecté en entrée du récepteur
n'est pas exactement
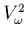 puisqu'il dépend aussi des impédances du
récepteur et de l'antenne. On verra plus de détails
dans la section 1.2, mais notons que la référence de base pour
ces calculs de bruit thermique pour différents types d'antenne est:
Tool Kit Antennae and Thermal Noise Near the Plasma Frequency,
N. Meyer-Vernet and C. Perche, Journal of Geophysical Research, Vol.94,
pp 2405-2415, 1989.
puisqu'il dépend aussi des impédances du
récepteur et de l'antenne. On verra plus de détails
dans la section 1.2, mais notons que la référence de base pour
ces calculs de bruit thermique pour différents types d'antenne est:
Tool Kit Antennae and Thermal Noise Near the Plasma Frequency,
N. Meyer-Vernet and C. Perche, Journal of Geophysical Research, Vol.94,
pp 2405-2415, 1989.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conditions1.2
- on verra
qu'essentiellement l'antenne doit être plusieurs fois plus longue que la
longueur de Debye
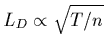 pour résonner aux ondes de Langmuir.
pour résonner aux ondes de Langmuir.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... maxwellienne1.3
- en général,
on utilise une distribution c÷ur+halo;
comme il ne s'agit
pas d'une distribution exactement maxwellienne, on parle alors de bruit
quasi-thermique
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... numérique1.4
- On utilisera ici
Numerical Recipes in Fortran(90) - The Art of Scientific Computing,
W.H Press, S.A. Teukolsky, W.T. Vetterling and B.P. Flannery
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mission1.5
- Ulysse a été lancé
fin 1990, est opérationnel actuellement et sa mission devrait officiellement
s'achever en 2002
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Z)1.6
-
qui ne présente pas d'intérêt pour notre étude,
sinon que son signal est
(malheureusement) quelquefois sommé à celui de l'antenne S
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Meudon1.7
- précisément au
Département de Recherche Spatiale
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... froids1.8
- Notons que le diagnostic du bruit quasi-thermique peut être
étendu (cf figure 1.1) à l'estimation de la
vitesse du vent solaire (dont
les équations (1.1) et (1.2) dépendent) en tenant compte
du bruit thermique
des protons décalé Doppler (au dessous de la fréquence plasma).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... brin1.9
-
cette approximation est valide dès lors que
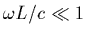 et que
et que
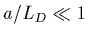
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... plasmas1.10
- ou des gaz
neutres (poser
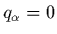 ): les équations de Navier-Stokes ou des
``fluides classiques'' ne sont en fait qu'une approximation ``continue''
de l'équation de Boltzmann
): les équations de Navier-Stokes ou des
``fluides classiques'' ne sont en fait qu'une approximation ``continue''
de l'équation de Boltzmann
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... moments1.11
-
le moment d'ordre
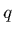 d'une distribution
d'une distribution 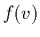 est formellement
est formellement
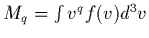 ; la densité est le moment d'ordre 0
; la densité est le moment d'ordre 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... diélectrique1.12
- c'est pourquoi on parle aussi pour
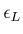 de
fonction diélectrique du plasma
de
fonction diélectrique du plasma
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... amorties1.13
- notons que les modes faiblement amortis se caractérisent par
une fréquence complexe de partie imaginaire négative ou nulle (sinon
il y a instabilité)
et telle que
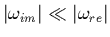
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
utilisant1.14
- poser
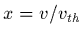 et calculer sur un contour entourant
et calculer sur un contour entourant
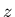 (dit contour de Landau) le prolongement analytique, dans le demi-plan
complexe
(dit contour de Landau) le prolongement analytique, dans le demi-plan
complexe
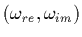 des ondes stables,
de la fonction
des ondes stables,
de la fonction
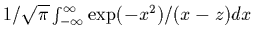 ,
dite fonction de dispersion des plasmas
,
dite fonction de dispersion des plasmas
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... []1.15
-
Quasi-thermal noise in a drifting plasma: Theory and application to
solar wind diagnostic on Ulysses,
K. Issautier et al., Journal of Geophysical Research, Vol.104,
pp 6691-6704, 1999.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fastidieux1.16
- c'est un cas où on peut se faire
aider par on progiciel de calcul symbolique
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fréquences)1.17
- en particulier on
n'ajustera ce modèle aux spectres radio d'Ulysse qu'à partir des
fréquences
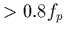
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
cas1.18
- précautions qui
s'imposent plus généralement à toutes les
méthodes de calcul dites "par différences finies".
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cas1.19
- citons par exemple l'interpolation par un polynôme de
Chebyshev, ou l'interpolation cubique spline -utilisée actuellement pour
les traitements QTN d'Ulysse au Despa
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quadratique2.1
- en anglais merit function
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... chi-carré2.2
- on parle alors de
chi-carré pour
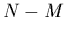 degrés de liberté
degrés de liberté
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... critère2.3
- un critère un peu
plus précis est: si la moyenne du
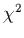 est
est 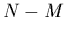 et son écart-type
et son écart-type
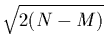
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fonctions2.4
- qui peuvent être
sauvagement non-linéaires en
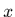 , le terme linéaire s'appliquant ici à
la dépendance du modèle par rapport aux paramètres
, le terme linéaire s'appliquant ici à
la dépendance du modèle par rapport aux paramètres 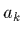
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... adaptée2.5
- par exemple par une
factorisation ``LU'' ou par la méthode de Cholesky puisque
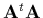 est une matrice définie positive - mais la méthode de Gauss-Jordan aura
l'avantage de calculer explicitement la matrice de covariance
est une matrice définie positive - mais la méthode de Gauss-Jordan aura
l'avantage de calculer explicitement la matrice de covariance
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...invhess).
2.6
- Reste à traduire toute cette stratégie numérique sous forme
d'un programme efficace, ce qui est par exemple bien fait dans la subroutine
(fortran) MRQMIN de Numerical Recipes, pp680-682.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... normale2.7
- on montre plus généralement que si
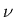 composantes sont fixées, le
composantes sont fixées, le
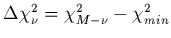 est distribué selon une distribution en chi-carré à
est distribué selon une distribution en chi-carré à 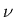 degrés de
liberté (et dans le cas étudié ici
degrés de
liberté (et dans le cas étudié ici 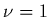 )
)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.