Principe des travaux virtuels
Ce principe peut s'énoncer ainsi:
lorsqu'on considère un champ de déplacement test ![]() défini
sur le volume
défini
sur le volume ![]() (nul sur
(nul sur ![]() ), alors la somme des travaux
«virtuels»
opérés lors de ce déplacement par
toutes les forces extérieures et intérieures au système est égale au
travail virtuel des quantités d'accélération, c'est-à-dire nul
si le système est à
l'équilibre statique. Autrement dit, en élastostatique, le travail virtuel des
efforts internes générés par les contraintes (dues à
l'élasticité/rigidité du solide) doit
compenser exactement le travail virtuel des efforts externes, ce
qui s'écrit au vu de (49)
), alors la somme des travaux
«virtuels»
opérés lors de ce déplacement par
toutes les forces extérieures et intérieures au système est égale au
travail virtuel des quantités d'accélération, c'est-à-dire nul
si le système est à
l'équilibre statique. Autrement dit, en élastostatique, le travail virtuel des
efforts internes générés par les contraintes (dues à
l'élasticité/rigidité du solide) doit
compenser exactement le travail virtuel des efforts externes, ce
qui s'écrit au vu de (49)
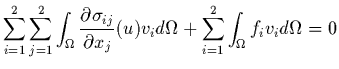 |
(53) |
La résolution du problème initial va donc se traduire par:
-trouver un déplacement ![]() défini sur
défini sur ![]() , nul sur
, nul sur ![]() ,
tel que
,
tel que ![]() , quelque soit
, quelque soit ![]() défini sur
défini sur
![]() , nul sur
, nul sur ![]() . Sous des hypothèses de régularités des
données (géométriques et physiques) toujours vérifiées dans la
pratique et en particulier dans le cas qui nous occupe, la théorie assure
l'existence et l'unicité d'une solution
. Sous des hypothèses de régularités des
données (géométriques et physiques) toujours vérifiées dans la
pratique et en particulier dans le cas qui nous occupe, la théorie assure
l'existence et l'unicité d'une solution ![]() (théorème de Lax-Milgram).
(théorème de Lax-Milgram).
Il ne reste plus qu'à discrétiser l'espace vectoriel des champs de
déplacement défini ci-dessus, c'est-à-dire poser le problème
linéaire ![]() , qui est posé a priori dans un espace vectoriel de
dimensions infinies, sous la forme d'un problème linéaire en dimensions
finies, qui s'écrira alors
, qui est posé a priori dans un espace vectoriel de
dimensions infinies, sous la forme d'un problème linéaire en dimensions
finies, qui s'écrira alors ![]() , où est une matrice carrée de
dimension finie
, où est une matrice carrée de
dimension finie ![]() (dite «matrice de rigidité») et
(dite «matrice de rigidité») et ![]() (inconnue) et
(inconnue) et
![]() (second membre dépendant des conditions aux limites) sont des vecteurs
de dimension
(second membre dépendant des conditions aux limites) sont des vecteurs
de dimension ![]() : c'est l'objet de la méthode dite
«des éléments finis»
: c'est l'objet de la méthode dite
«des éléments finis»