Une esquisse de la théorie cinétique des plasmas
Sous certains aspects, un plasma est un fluide parfait conducteur,
c'est-à-dire
qu'il peut être modélisé comme s'il s'agissait d'un milieu continu (
voir le
premier chapitre de ce cours), c'est-à-dire par les équations qui
régissent les fluides classiques,
auxquelles on ajoute les équations de Maxwell, la loi d'Ohm
et l'action des forces de Lorentz, pour obtenir
les équations de la magnétohydrodynamique ou MHD.
Cependant, de nombreuses propriétés des plasmas (en
particulier des plasma ``chauds'') ne peuvent
être abordés par la MHD et leurs propriétés n'apparaissent
seulement qu'au travers de leur
comportement microscopique. Ces comportements sont mieux modélisé par
les méthodes
de la théorie cinétique, c'est-à-dire les méthodes qui
prennent en compte le mouvement de chacune des particules qui composent
le plasma : le milieu est dit alors discret ou particulaire.
Pour pouvoir ensuite accéder avec de tels modèles aux quantités
macroscopiques, on a recours aux méthodes statistiques. L'outil de base
pour la description d'un modèle cinétique en ![]() et à l'instant
et à l'instant
![]() est la fonction de distribution
des vitesses de particules
est la fonction de distribution
des vitesses de particules
![]() .
.
L'équation de base de la théorie cinétique des plasmas1.10 faisant intervenir la fonction de
distribution des vitesses
est l'équation de Boltzmann, qui s'écrit sous sa forme non-relativiste
et pour une espèce ![]() de particules de distribution
de particules de distribution ![]() :
:
 |
(1.10) |
Dynamique électrostatique, linéarisée, à une dimension
On voit sur le dernier terme de (1.9) que les équations du
modèle de Vlasov-Maxwell sont non-linéaires et donc en général
difficiles à résoudre analytiquement.
C'est pourquoi, et cela suffira pour le projet de modélisation du bruit
thermique, nous allons les réduire à une dimension (ce qui revient à
considérer un plasma isotrope) et se restreindre aux ondes purement
électrostatiques ![]() .
.
Soit ![]() la coordonnée dans le système à une dimension étudié.
En posant
la coordonnée dans le système à une dimension étudié.
En posant
![]() , et
, et ![]() , on a
d'après (1.9)-(1.14):
, on a
d'après (1.9)-(1.14):
| (1.18) | |||
| (1.19) |
On résout ensuite les équations (1.20)-(1.22)
comme suit: On transforme par Fourier les champs de perturbation
dépendant de l'espace et du temps, de sorte que
(1.20)-(1.22) deviennent des équations linéaires
algébriques dans l'espace spectral ![]() qui se résolvent facilement.
Les dépendances
spatio-temporelles des champs sont ensuite obtenues en inversant la
transformation de Fourier. Les transformées de Fourier de
(1.20)-(1.22) s'écrivent:
qui se résolvent facilement.
Les dépendances
spatio-temporelles des champs sont ensuite obtenues en inversant la
transformation de Fourier. Les transformées de Fourier de
(1.20)-(1.22) s'écrivent:
 |
(1.26) |
On voit qu'il y a deux parties dans la densité de charge ![]() ,
dont une seule dépend du champ électrique
,
dont une seule dépend du champ électrique ![]() appelée
densité de charge collective:
appelée
densité de charge collective:
La permittivité longitudinale du plasma
La dynamique des perturbations du plasma décrite par l'équation de
Vlasov linéarisée fait correspondre à un champ électrique
donné ![]() une densité de charge collective. Cela permet de définir
une fonction de réponse interne, la susceptibilité longitudinale
une densité de charge collective. Cela permet de définir
une fonction de réponse interne, la susceptibilité longitudinale
![]() par la formule:
par la formule:
 |
(1.31) |
Comme chaque espèce de particule du plasma contribue indépendamment
à la densité, on peut définir la susceptibilité longitudinale de
chaque espèce simplement par:
En portant (1.30) dans (1.29) qui décrit le champ électrique
engendré par des excitations extérieures, on a:
l'équation (1.33) montre que, comme dans un diélectrique
1.12ordinaire, la permittivité
![]() tend à
faire ``écran'' au champ d'excitation extérieur
tend à
faire ``écran'' au champ d'excitation extérieur ![]() .
Mais la permittivité d'un plasma n'est pas une constante, elle varie
avec
.
Mais la permittivité d'un plasma n'est pas une constante, elle varie
avec ![]() et
et ![]() , ce qui se traduit par le fait que le plasma
est un milieu dispersif, temporellement et spatialement. Autrement dit,
, ce qui se traduit par le fait que le plasma
est un milieu dispersif, temporellement et spatialement. Autrement dit,
![]() agit comme un ``écran dynamique'' vis-à-vis
du champ d'excitation.
agit comme un ``écran dynamique'' vis-à-vis
du champ d'excitation.
Ondes longitudinales électrostatiques
L'étude de la dynamique non collisionnelle à une dimension
qui précède
peut aussi s'appliquer dans un plasma réel (à trois dimensions)
à condition de se restreindre à des fonctions de
distributions d'équilibre isotropes, c'est-à-dire telle que
![]() et restreindre
l'espace
et restreindre
l'espace
![]() aux seules ondes longitudinales électrostatiques,
c'est-à-dire telles que
aux seules ondes longitudinales électrostatiques,
c'est-à-dire telles que
![]() .
Puisque
.
Puisque ![]() et
et ![]() ont des directions relatives arbitraires,
on note
ont des directions relatives arbitraires,
on note ![]() la composante de
la composante de ![]() parallèle à
parallèle à ![]() et
on introduit les fonctions de distribution scalaires réduites:
et
on introduit les fonctions de distribution scalaires réduites:

Ondes électrostatiques dans un plasma maxwellien
Quand les fonctions de distribution d'équilibre des particules du plasma sont maxwelliennes, on peut obtenir des expressions analytiques explicites de la relation de dispersion des ondes faiblement amorties 1.13. Les ondes électrostatiques dans un plasma non magnétisé ou peu magnétisé comme le vent solaire peuvent être séparées en deux familles: les ondes de hautes fréquences (près de la fréquence plasma des électrons) -celles qui vont nous intéresser ici- appelées ondes de plasma électroniques (ou oscillation de plasma, ou ondes de Langmuir) pour lesquelles le mouvement des ions est négligeable; les ondes de basse fréquences (sous la fréquence plasma des ions), appelées ondes acoustiques ioniques ou pseudo-sonores.
On va donc négliger le mouvement des ions et on a seulement besoin de
considérer la fonction de distribution à l'équilibre ![]() des
électrons. Dans le cas réduit à une dimension, on aura:
des
électrons. Dans le cas réduit à une dimension, on aura:
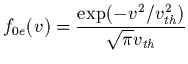 |
(1.35) |