

Next: 0.1.3 Cas d'un fluide
Up: 0.1 Fluides classiques et
Previous: 0.1.1 Introduction
La loi d'état d'un milieu incompressible s'écrit
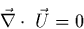 |
(6) |
Cette incompressibilité et l'homogénéité (i.e.  est invariant
par rapport à l'espace)
du fluide font que la conservation de la masse signifie simplement
est invariant
par rapport à l'espace)
du fluide font que la conservation de la masse signifie simplement
 constante et que le tenseur des contraintes est réduit
à :
constante et que le tenseur des contraintes est réduit
à :
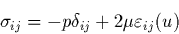 |
(7) |
d'où la nouvelle forme de (2):
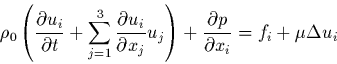 |
(8) |
ou son expression vectorielle 3 :
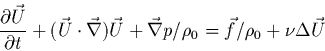 |
(9) |
où
 est la viscosité cinématique du
fluide.
est la viscosité cinématique du
fluide.
Le système d'équations non-linéaire {(6),(9)} est
connu sous le nom de Navier-Stokes; il comporte quatre équations aux
dérivées partielles (dont trois du second ordre) pour la
détermination de quatre inconnues:
 et
et  , des
données initiales sur
, des
données initiales sur  et
et  et les conditions aux limites
de type (4),(5), plus éventuellement des conditions de
continuité si la frontière
et les conditions aux limites
de type (4),(5), plus éventuellement des conditions de
continuité si la frontière  comporte une surface libre (voir
note 2).
comporte une surface libre (voir
note 2).

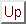

Next: 0.1.3 Cas d'un fluide
Up: 0.1 Fluides classiques et
Previous: 0.1.1 Introduction
Michel Moncuquet
DESPA, Observatoire de Paris
2001-03-05
![]() et
et ![]() , des
données initiales sur
, des
données initiales sur ![]() et
et ![]() et les conditions aux limites
de type (4),(5), plus éventuellement des conditions de
continuité si la frontière
et les conditions aux limites
de type (4),(5), plus éventuellement des conditions de
continuité si la frontière ![]() comporte une surface libre (voir
note 2).
comporte une surface libre (voir
note 2).