4.2.1 Electron density from the IPT passes

In Figure 5 we show the comparison of electron densities measured by Voyager 1, Voyager 2, Ulysses and Galileo with the predictions at the spacecraft locations from the (i)Maxwellian isotropic, (ii)near isotropic bi-kappa model ( $\kappa_i=2,A_{0}=1.2$ for all species) or (iii) anisotropic bi-kappa model ( $\kappa_i=2,A_{0i}=3$) based on Voyager 1 inbound plasma conditions (referenced hereinafter as case (i),(ii) or (iii)). The match of the model to data obtained in March, 1979, July 1979 and February 1992 is remarkable considering we are using an azimuthally-symmetric model with a single value of kappa for all ions and that the values of kappa and anisotropy are assumed to be constant throughout the torus.

Figure 5: Comparison of computed models (colored lines) with measurements(black lines) of electron density from Voyager 1 and 2, Ulysses and Galileo. The Voyager 1 inbound density profile is shown only with the reference data set (dashed-dotted green line) which is used for building the other profiles. The predicted profiles have been superposed on the data as:
-blue in case of the Maxwellian isotropic model
-orange in case of the bi-kappa model with $\kappa _i=2, \kappa _e=2.4, A_{0i}=A_{0e}=1.2$
-red in case of the bi-kappa model with $A_{0i}=3$ and all other parameters as above.
(Notes: for Ulysses, the density profiles have been multiplied by 1.9. The Log-vertical(density) ranges are not the same for all panels)

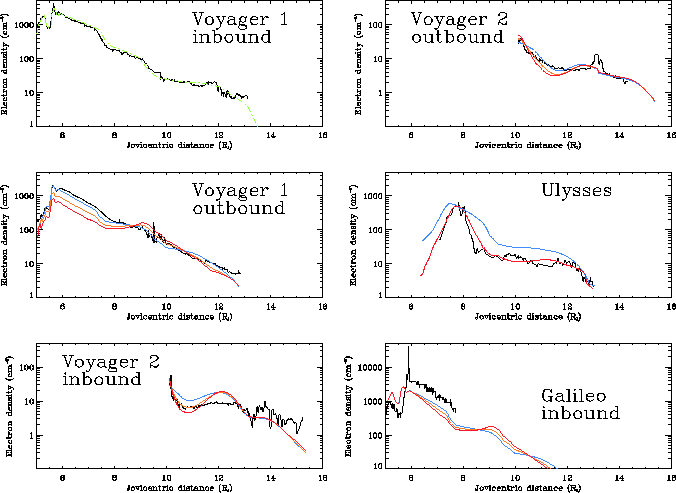
To match the Ulysses measurements we had to enhance the total charge density throughout the torus by a factor of 1.9 compared with the Voyager epoch. This enhancement is comparable to the higher overall densities measured by Galileo in 1995 [ Frank et al., 1996, Gurnett et al., 1996, Bagenal et al., 1997]. The Ulysses measurement of the tight confinement of the density to the equator (illustrated by the narrow peak around 8${\rm R_J}$) could not be matched by using an isotropic kappa, nor by a highly anisotropic ($A>10$) bi-Maxwellian. On the other hand, after selecting a normalization factor (1.9) and values of $\kappa$ and $A_{0}$ to match the equatorial confinement, the densities were also very well matched beyond 9${\rm R_J}$ when Ulysses was at high latitudes. The model/data rms is $\sim 60\%$ for case (iii), 270% for case (i).

When comparing the model (based on Voyager 1 inbound conditions) with the densities measured on the Voyager 1 outbound passage, we see that the densities beyond 9${\rm R_J}$ match very well, but in the main part of the torus the observed densities are about a factor of 3 higher than predicted by the anisotropic ($A=3$) bi-kappa model. Since the latitudinal ranges of the inbound and outbound passes are similar, this substantial difference in density level suggests a strong longitudinal asymmetry in the torus. This asymmetry had already been noted from comparison with previous models by Hoang et al. [1993]. When we compare the longitude of the spacecraft with the longitudinal variations in emission intensity observed by Schneider and Trauger [1995], however, we find that the ground based emissions predict the opposite of what was observed (namely, that the outbound densities should have been lower rather than higher than those based on the inbound observations). Of course, this might also suggest that the temperature anisotropy is not constant throughout the torus but instead weaker between 6 to 9${\rm R_J}$ than beyond. It is also worth noting that the isotropic Maxwellian provides a significantly better fit in this region than either of the kappa distributions, with a model/data rms of $\sim 17\%$, against 26% for case (ii) and 36% for case (iii).

When comparing the model with the Voyager 2 data (from [ Belcher, 1983, figure 3.14]), obtained 6 months after Voyager 1, we find that the bi-kappa model, without any normalization factor, matches the densities at closest approach to Jupiter which occurred close to the equator at about 10${\rm R_J}$. The model/data rms are: on inbound for cases (i) 68%, (ii) 48%, (iii) 56% and on outbound for cases (i) 29%, (ii) 25%, (iii) 34%. More precisely, a quasi isotropic ($A=1.2$) kappa model ($\kappa=2$) yields the correct density gradient when the spacecraft comes (inbound as well as outbound) from the centrifugal equator up to higher latitudes (with a maximum at $\sim 13\hbox{$^\circ$}$ south) at a Jovicentric distance of $\sim 11{\rm R_J}$ (see Figure 1). On the inbound trajectory, however, when the spacecraft is close to the equator again, say around $12{\rm R_J}$, the model over-predicts the observations by about a factor of 2. In contrast, the model under-predicts the observations by about the same factor beyond $13{\rm R_J}$, when the spacecraft returned to high latitudes. This difference might be explained by the plasma being hotter (and thus spread farther from the equator) at the time of Voyager 2. A hotter plasma at the time of Voyager 2 is consistent with higher electron temperatures inferred from UV emissions by Sandel et al. [1979]. On the other hand, the differences might also be due to distortions in the magnetic field by a change in the equatorial current sheet, which can be significant beyond $10{\rm R_J}$.

We have also shown on Figure 5 the electron density profile (from [ Bagenal et al., 1997]) measured by Galileo during its pass through the torus on December 7th, 1995. In the outer part of the IPT, the electron density observed by Galileo is roughly a factor of two higher than the Voyager 1 value, and so about the same as the equatorial density inferred from Ulysses observations. Unfortunately, data are available only inward $<8{\rm R_J}$ and, because the Galileo inbound trajectory was very close to the centrifugal equator at these distances (see Figure 1), these data cannot be used to constrain our model. Let us remark, however, that the slope of the decreasing density with distance is better predicted with a near-isotropic kappa model (i.e. $A_0=1.2$ and $\kappa_i = 2$) than with a Maxwellian core+halo or with a higher anisotropy. It is also worth noting that all models fail to predict the magnitude of the ledge observed by Galileo near $5.8{\rm R_J}$, even ignoring the spike associated with the close approach to Io.