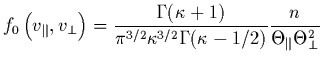3.3 Anisotropic Bi-kappa Ion Distributions

When dealing with non-thermal velocity distributions for the ion species, we must consider the issue of their thermal anisotropy, i.e. the difference in temperature parallel and perpendicular to the magnetic field and the concomitant magnetic mirror force. Unfortunately, the Voyager PLS instrument was only able to measure the perpendicular temperature of the ions. The results reported by Bagenal [1994] were consistent with a perpendicular velocity distribution of the ions having a thermal core with a non-thermal ``tail'' or ``halo''. The Galileo plasma instrument has a full angular response and indicated that the thermal core of the ion distribution is isotropic [ Crary et al., 1998]. In contrast, there is good reason to believe that the halo component of the ion distribution should be highly anisotropic. When neutral atoms (escaped from Io's atmosphere) are first ionized they experience Jupiter's strong magnetic field and ``pick-up'' a gyro-motion perpendicular to the magnetic field equal to the bulk (corotation) speed of the plasma. The initial parallel motion of the pick-up ions is small. Hence, we might expect that a population of freshly-ionized particles would have a highly anisotropic distribution. Eventually, one expects these pick-up ions to be partially thermalized by plasma waves and, on longer time scales, by collisions. While the time scales for partial thermalization of such a ``ring'' distribution are not well known, it is clear that we should expect a substantial anisotropic supra-thermal component for the ion velocity distribution.

For the purposes of modeling an anisotropic distribution having a suprathermal tail, we adapt an anisotropic kappa distribution from [ Summers and Thorne, 1992], which we call bi-kappa (by analogy to bi-Maxwellians) and is of the form:

$$f_0\left( v_{\parallel},v_{\perp} \right) = \frac{\Gamma(\kappa +... ...appa^{3/2}\Gamma(\kappa -1/2)} \frac{n}{ \Theta_{\parallel} \Theta_{\perp}^{2}}$$

$$\times \left[ 1+ \frac{v_{\parallel}^{2}}{\kappa \Theta_{\parallel}^{2}} + \frac{v_{\perp}^{2}}{\kappa \Theta_{\perp}^{2}} \right]^{-\kappa -1}$$ (8)

Applying Liouville's theorem with the conservation of energy and magnetic moment ( $\mu \propto v^2_{\perp}/B$), as in the isotropic case, one derives the density distribution for each particle species. Recall that Liouville's theorem allows one to express the distribution as a function of the curvilinear co-ordinate $s$ along the magnetic field, in the presence of a monotonic attractive potential $\Phi(s)$, as

$$f(s,v,v_\perp^2) = f_0\left(\sqrt{v^2+ 2\frac{\Phi(s)}{m}}~,~v_{\perp}^2 \frac{B(0)}{B(s)}\right)$$ (9)

By expressing the thermal anisotropy at the equator as $A_0=\Theta_{\perp}^2/\Theta_{\parallel}^2=T_{\perp}(0)/T_{\parallel}(0)$ we can use (9) to calculate the moments of the distributions to derive the latitudinal profiles of density and temperature as follows:

$$\frac{n(s)}{n(0)} = {\left[ 1+\frac{2\Phi(s)}{m \kappa \Theta_{\p... ...right]} ^{\frac{1}{2} - \kappa} \frac{1}{A_0+(1-A_0)\frac{B(0)}{B(s)}} \protect$$ (10)

$$\frac{T_{\parallel}(s)}{T_{\parallel}(0)} = {\left[ 1+\frac{2\Phi... ...,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ \protect$$ (11)

$$\frac{T_{\perp}(s)}{T_{\perp}(0)} = {\left[ 1+\frac{2\Phi(s)}{m \... ... \Theta_{\parallel}^2} \right]} \frac{1}{A_0+(1-A_0)\frac{B(0)}{B(s)}} \protect$$ (12)

When $\kappa \mapsto \infty$, one retrieves the results obtained with a bi-Maxwellian distribution of Huang and Birmingham [1992]. In this case, we get, from equation 12 with $A_{0}>1$ (as expected in the torus -see the above discussion), a perpendicular temperature which decreases with latitude and, from (11), a constant parallel temperature. When $A_0=1$ (isotropy), one retrieves the density profile (4) found by Meyer-Vernet, Moncuquet and Hoang [1995].

Note that with these bi-kappa distributions neither the parallel nor the perpendicular temperature strictly follow a polytropic law. The parallel temperature increases with latitude independently of $B$ while the perpendicular one has an additional variation along the magnetic field due to the change in field strength. This means that the anisotropy is not constant along magnetic field lines, but decreases if $A_{0}>1$. Since the change in magnetic field strength is small ($<$20% over the latitudinal range of Ulysses) this is a minor effect, unless the anisotropy at the equator is particularly strong.

To illustrate the relative effects of the anisotropy and of the suprathermal tail, we show in Figure 3 several latitudinal density profiles calculated with different values of the parameters $A_0$ and $\kappa$.

Figure 3: Plasma density (normalized to the centrifugal equator) as a function of the magnetic latitude (Jovian tilted dipole model), for two kappa values (2 and 4) of the velocity distribution of a typical ion of the Io torus ( $m_i = 20 m_p, Z_i=+1$), and compared to the density profile obtained with a Maxwellian distribution ( $\kappa_i \mapsto \infty$). The bold curves are isotropic distributions, the thin curves have a temperature anisotropy $T_{\perp }/T_{\parallel }=3$ ( NB: in all cases, the kappa of the electrons was set to 2.4 [ Meyer-Vernet et al.,1995] and their anisotropy to 1.2 [ Sittler and Strobel, 1987]).

We chose a longitude (201$^\circ$) where the magnetic and rotational equators are separated by the maximum amount (9.6$^\circ$) to illustrate the limited influence of the changing magnetic field strength on the density distribution. The density maximum is located at the centrifugal equator (at a magnetic latitude of 9.6/3 = 3.2$^\circ$) and the net effect of the magnetic mirror force is a small asymmetry about the centrifugal equator.

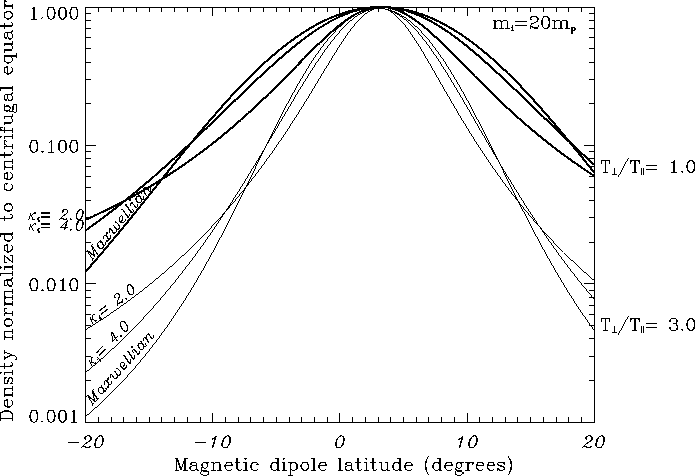The profiles in Figure 3 were obtained by solving equation (10) for both the electrons and a single ion species with the equation of charge neutrality $n_e(s)/n_e(0)=n_i(s)/n_i(0)$ which permits the elimination of the electric potential $\phi _E$. One can see that the kappa distributions have the tendency to tightly confine the particles to the equator while allowing a substantial population at high latitudes. The effect of increasing the thermal anisotropy ($A_0=1$ to 3), for either the Maxwellian or kappa cases, is to further confine the plasma to the equator.

With these tools in hand, including the flexibility of varying the unknown parameters $A_0$ and $\kappa$, we are now able to model the density distributions observed by different spacecraft as they traversed the torus.