Rappelons tout d'abord que la densité
spectrale d'un signal
est donnée par la transformée de Fourier de sa fonction d'autocorrélation.
Si ce signal est la tension recueillie
aux bornes d'une antenne immergée dans un plasma -le vent solaire-
ayant une vitesse d'expansion 
, et en notant 
la T.F de la distribution de courant le long de l'antenne d'une part et
la fonction d'autocorrélation du champ électrostatique variable
vu par l'antenne d'autre part, on aura :
À des fréquences très supérieures à la fréquence gyromagnétique (sans quoi, on peut voir par exemple le chapitre ii de la thèse), on a :
étant la distribution de vitesse de la
espèce de charge 
,
et 
la fonction diélectrique longitudinale du plasma.
Le terme 
dépend de la forme et de la direction de
l'antenne, et le signal
réel collecté en entrée du récepteur n'est pas exactement 
puisqu'il dépend aussi des impédances du
récepteur et de l'antenne [Meyer-Vernet and Perche, 1989, pour plus de détails, voir,].
On veut surtout ici montrer l'équation A.2 qui permet de comprendre
pourquoi on peut, moyennant un certain nombre de conditions
satisfaites par l'instrument URAP d'Ulysse dans le vent solaire,
«remonter»
à la distribution de vitesse des électrons et fournir un diagnostic assez
précis des densités et températures du plasma ambiant.
En pratique, on procède de la façon suivante :
on se donne un modèle de distribution des vitesses du plasma
que l'on veut mesurer (en général, une distribution coeur+halo;
comme il ne s'agit
pas d'une distribution exactement maxwellienne, on parle alors de bruit
quasi-thermique), on calcule la densité spectrale aux bornes de l'antenne
en utilisant notamment les équation ci-dessus, et on déduit les paramètres
du plasma en ajustant le modèle aux spectres observés.
Notons que ni le calcul théorique [Meyer-Vernet and Perche, 1989], ni la
méthode d'ajustement aux spectres expérimentaux
[voir l'appendice du papier Maksimovic et al.
référencé ci-contre] ne sont complètement immédiats.
Dans le vent solaire et avec une distribution core+halo, les paramètres
les mieux déterminés sont la densité totale (à 
) et la température
des froids (mieux que 15%).
Le diagnostic de la densité totale des électrons est excellent
car, à la fréquence plasma, qui est un zéro de
la fonction diélectrique 
, le bruit s'accroît considérablement
(quelle que soit la distribution, voir Éq.A.2),
formant un pic de puissance très marqué sur chaque spectre et, sur les
spectrogrammes, une
«ligne» continue fort intense par rapport au bruit de fond
que l'on peut suivre très nettement sur la figure A.2. Le diagnostic de
température nécessite par contre, via l'ajustement, de connaître la
forme précise du spectre immédiatement en amont et, sur une large
gamme, en aval de la fréquence plasma. Par exemple, sur la figure A.2,
on ne pourra pas porter de diagnostic de température précis pendant la
période allant d'environ 8 à 11 heures T.U, car un type III solaire très
intense vient polluer les spectres de bruit quasi-thermique au-dessus de la
fréquence plasma (qui reste cependant très visible car elle se comporte comme
une fréquence de coupure vis-à-vis de l'émission type III solaire).
Notons enfin que le diagnostic du bruit quasi-thermique a été récemment étendu à l'estimation de la vitesse du vent solaire (dont les équations A.1 et A.2 dépendent) par la modélisation et ajustement aux spectres d'Ulysse du bruit thermique des protons décalé Doppler (au dessous de la fréquence plasma) [voir les articles d'Issautier et al. référencés ci-dessous].
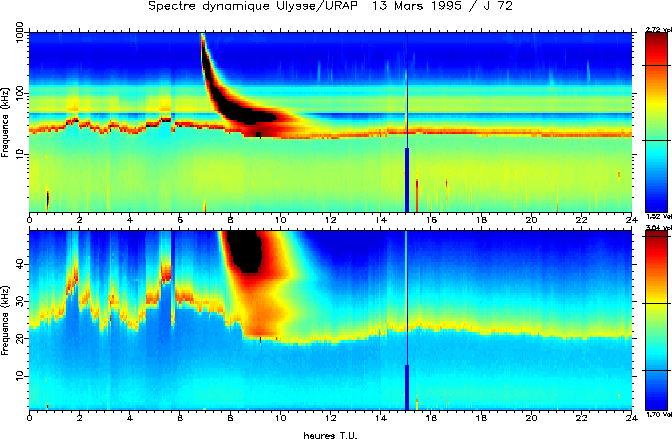
Figure A.2: Spectre dynamique de routine obtenu par Ulysse durant la
journée du 13 mars 1995, dans le vent solaire
Petite bibliographie chronologique des principaux papiers relatifs à l'analyse du bruit quasi-thermique sur Ulysse dans le vent solaire :
S. Hoang, N. Meyer-Vernet, J-L Bougeret, C.C. Harvey, C. Lacombe, A. Mangeney, M. Moncuquet, C. Perche, J-L Steinberg, R.J. MacDowall, R.G. Stone, Solar wind thermal electrons in the Ecliptic plane between 1 and 4 AU: Preliminary results from the Ulysses Radio Receiver, Geophys. Res. Lett., 19, 1295-1298, 1992.
M. Maksimovic, S. Hoang, N. Meyer-Vernet, M. Moncuquet, J-L Bougeret, J.L. Phillips, P. Canu, The solar wind electron parameters from quasi-thermal noise spectroscopy, and comparison with other measurements on Ulysses, J. Geophys. Res., 100, 19881-19891, 1995.
S. Hoang, N. Meyer-Vernet, K. Issautier, M. Maksimovic, M. Moncuquet, Latitude dependence of Solar Wind plasma thermal noise: Ulysses radio observations, Astron. Astrophys., 316, 430-434, 1996.
K. Issautier, N. Meyer-Vernet, M. Moncuquet, S. Hoang, Solar wind radial and latitudinal structure : electron density and core temperature from Ulysses thermal noise spectroscopy, J. Geophys. Res. à paraître, 1998.
