Bernstein waves are electrostatic waves, sustained by the electron gyration in
the ambient magnetic field 
, which propagate without damping between
gyroharmonics, perpendicular to ( 
hereinafter,
see section 4.4).
Their wavelength is of the order of 
times the electron
gyroradius. True Bernstein waves [Bernstein, 1958] correspond
to the ideal case of a Maxwellian electron plasma described by the Vlasov
equation. However, the electron velocity distribution in the Io torus cannot be
accurately fitted by one Maxwellian [Scudder, Sittler and Bridge, 1981]
and was not measured by Ulysses in this region. Hence, following [Sittler and Strobel, 1987], we shall use the convenient distribution made of
two Maxwellians, describing hot and cold populations. Since the measured
electrostatic field is very stable, without sporadic emissions,
and the level is compatible with QTN in a stable plasma, we do not
consider complex unstable distributions (see section 4.4).
With such a core plus halo distribution,
the Bernstein's dispersion equation is
where 
is a modified Bessel function of the first kind and
the angular gyrofrequency.
Here 
and 
are
the density and the thermal
electron gyroradius, respectively, of each population (c,h ).
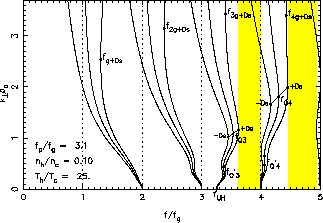
Figure 1: Example of Bernstein waves forbidden bands (grey strips).
The dispersion curves in the plasma frame are plotted as thick lines, the
Doppler-shifted ones are plotted as thin lines.
The resonances ( 
) are indicated by
dots. The locus of all 
contributing to the quasi-thermal noise level
is shown as a
segment from 
to 
Figure 1 shows some examples of Bernstein wave dispersion
curves computed from (1) in the range 
with
, which is typical of the
spectra observed by Ulysses between 
and 
,
and 
and 
, which is of the order of the values measured
by Voyager 1 in that region [Sittler and Strobel, 1987].
The resonances are the finite solutions of the dispersion equation
(1)
where the group velocity 
vanishes
(except
the solution at 
, which is the upper hybrid frequency 
).
As is well known [see, e.g., [Belmont, 1981]], the presence
of the hot population may bring about a secondary resonance
(noted 
in the nth intraharmonic band)
which occurs, in the parameter ranges considered here, below the
linked to the main cold population.
We also show as thin lines in Figure 1 Doppler shifted dispersion
curves occurring in the frame of an antenna with a relative velocity 
.
These curves were computed by substituting for 
the term
in (1), using 
km/s as measured by [Stone et al., 1992b] and 
K as measured by
[Moncuquet, Meyer-Vernet and Hoang, 1995] near 
;
they bracket the solutions of (1)
contributing to the QTN (see section 3).
The Doppler shift of Bernstein waves has two consequences for
large 
in each gyroharmonic band:
(1)resonant modes (where 
vanishes) can exist above the exact
gyroharmonic (they are noted 
in Figure 1) and (2)
nonresonant modes can be present below the exact gyroharmonic.
In the gyroharmonic band and in the bands above,
there always exists a ``forbidden band'' for Bernstein modes, that is,
where (1) has no solution in the absence of Doppler shift.
That band is located between and the consecutive gyroharmonic
.
In the presence of a Doppler
shift, the largest occurs at a slightly larger frequency
(noted hereinafter), and
the band
is not fully forbidden since modes of very large exist. However,
this band is forbidden for resonant modes (note that its upper limit may be
just below the gyroharmonic, since the 
can be slightly shifted below ).
These forbidden bands are shown as grey strips in Figure 1.
