In a Maxwellian electron plasma described by the Vlasov equation, the dispersion equation of Bernstein waves can be put into the implicit form
where 
is a modified Bessel function of the first kind,
and 
are
the electron (angular)
plasma frequency and gyrofrequency, respectively, and 
is
the thermal electron gyroradius.
One can deduce from (B1) the two partial derivatives of
as a function of 
and 
:
Some samples of calculations using these equations are shown in Figure B1.
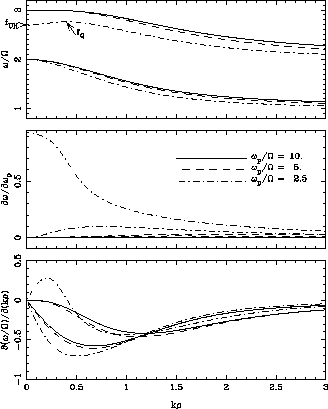
Figure B1: Dispersion characteristics of Bernstein waves. (top)
Classical dispersion curves deduced from
(B1) in
the two first intraharmonic bands for three typical values of 
,
involving the 
and 
frequencies in the case of 
.
(middle) The six corresponding derivatives with respect to
computed from (B2). Except for the band,
these derivatives become vanishingly small when the ratio increases.
(bottom) The six corresponding derivatives with respect to ,
computed from (B3).
Note that all infinite sums in the preceding equations are rather quickly convergent. A criterion to stop their calculation is that the last nth computed term in (B1) satisfies
with n>m, where m is the order of the upper limit of the band considered and
the precision to be achieved. For instance, in this paper, where
, 
, and 
,
such computations need 3<n<17 for 
.
Acknowledgments
The URAP experiment is a joint project of NASA GSFC, Observatoire de Paris,
CRPE, and the University of Minnesota. The Principal Investigator is R.G. Stone.
The French contribution was mainly financed by the Centre National d'Études
Spatiales.
We thank A. Balogh, Principal investigator, and R.J. Forsyth,
Co-Investigator, on the magnetometer experiment for kind permission to use their
data. We are very grateful to
R. Manning and the team of engineers and technicians of the Département de
Recherches Spatiales (Observatoire de Paris), who designed
and built the radio receiver whose great performances made possible this work.
We sincerely thank J.-L. Steinberg for a careful reading and helpful
comments on the manuscript.
The Editor thanks C.P. Paranicas and another referee for their
assistance in evaluating this paper.
