To compute the Doppler effect on the voltage power spectrum seen by the antenna,
we have to substitute in (1)
the electric field 
with
, where 
is the relative
velocity of the antenna with respect to the ambient plasma.
Since 
is roughly perpendicular to and
the angle between the spin plane of the antenna and the plane defined by
remains small ( 
), we may write
.
The solution 
of the dispersion equation in the presence of the relative
velocity will thus be modified from the nonshifted solution 
, as
with 
,
which reads
where we have set 
.
Now if we replace in (1) with , we obtain a
Doppler-corrected antenna response function:
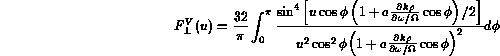
We may remark that 
is an even function of
with 
, so that
.
However, this factor
could take values close to 1, especially near the gyroharmonics where
, and so
we have numerically studied the variation of the function
with the variations of the plasma parameters involved in (A2).
During the IPT crossing, at a Jovicentric distance of about 8 
,
V is nearly the corotation velocity
[Stone et al., 1992b], which increases with the Jovicentric
distance from 
to 
km/s and the temperature
from 
near the torus equator to 
at
highest latitudes. These variations lead to a parameter a such that
0.05<a<0.1, and the derivative 
can be computed using (B3). This
derivative depends on the gyroradius, that is, on both the temperature and
the gyrofrequency 
which decreases with from 
to
kHz. All these variations cannot be easily summarized and have to
be computed for each spectrum. The result is that the difference between the
Doppler-affected modulation 
and
the modulation given by (2)
does not exceed in any cases 
for 
We show in Figure A1 a typical sample of the antenna response
with Doppler
effect computed from (A2), with a= 0.06 and 
.
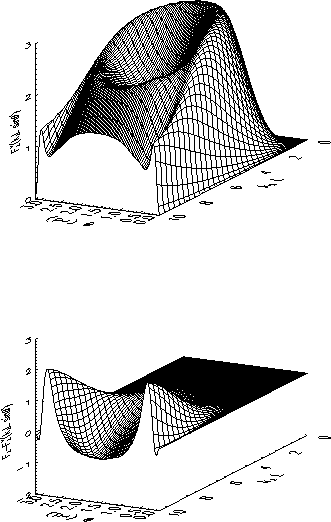
Figure A1: (top) Antenna response to Bernstein waves with Doppler effect
and (bottom) the difference with the antenna response without Doppler effect
shown in Figure 3
as a function of kL and the angle 
between the antenna and
the magnetic field (in radians).
