Now we want to exploit (3). We shall first remove
the effects of
the power spectrum variation between the gyroharmonics, which is not relevant
here; but we shall use the fact that the modulation is not the same during
each half-spin of the Ulysses antenna (see Figure 2)
thanks to the shape of 
shown in Figure 3.
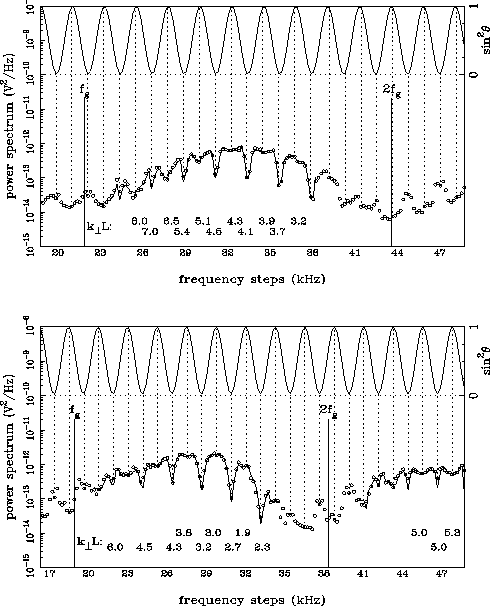
Figure 2: Two typical samples of spectra recorded on Ulysses
(1559:20 UT and 1628:08 UT on February 8, 1992) in the first gyroharmonic
band and the beginning of the second one.
The small circles are the measurements and the solid lines are the best fit
antenna response arch by arch
(one arch starting alternatively at a
minimum or at a maximum of sin 
, finishing at the consecutive
minimum or maximum, respectively,
and the signal correction described in the text is processed along each arch).
The corresponding values of 
are
indicated below. The angle 
between the antenna and the
magnetic field, plotted as sin 
at the top of each panel, is computed
using the magnetometer data (courtesy of A. Balogh).
The frequency step
incrementation (0.75 kHz) of the radio receiver appears as a thin,bold line
on the x axis.
As shown by [Meyer-Vernet, Hoang and Moncuquet, 1993],
the variation with is strongly sensitive to the value of
(except when 
). Whereas 
varies
as 
when , it has instead a minimum at
when 
, and this minimum becomes deeper as
increases. The magnetic field was simultaneously measured aboard
Ulysses [Balogh et al., 1992],
and we can thus deduce from
the observed spin modulation for the frequency band on which the receiver
is tuned during each half-spin of the antenna, so that we can finally
determine experimental dispersion curves (i.e., a set of points
) of electrostatic waves in the ambient plasma.
With this aim in view, we must first normalize the signal within each
arch of in order to suppress the part of
the variation which does not depend on the antenna response.
This is done by interpolating the signal (in logarithm) between
two consecutive equal values of
(involving an a priori choice of the starting points, see
Figure 2 caption)
and then substracting from the signal (in logarithm) the interpolated variation,
taking into account that the measurement is made by steps (four measurements
for each frequency during 2 s).
We then fit (by a least 
method on a logarithmic scale)
the antenna response
to the normalized signal. The fitting
method is
processed arch by arch (i.e., for varying in an interval
of width 
) and
with two free parameters: and a translation
parameter controlling the mean on one arch of the logarithmic power level,
which is arbitrary after the
above described normalization. This second parameter is introduced
in order to avoid any bias in the
determination linked to the normalization.
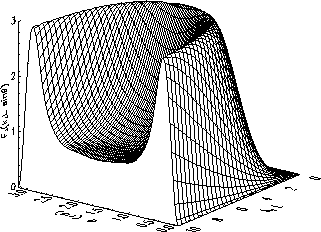
Figure 3: Antenna response to perpendicular waves plotted
as a function of and of the angle between the antenna and
the magnetic field (in radians). Whereas for 
, the response varies as (being maximum
for ), it has a minimum at for
, which becomes more and more pronounced as
increases.
Furthermore,
we compute the by using equal measurement errors 
( 
), except when 
which entails that
(1) is not valid. These points are
cancelled by setting the corresponding 
.
The minima are found using Levenberg-Marquart's method [see
[Press et al., 1992], and references therein], which also
provides
the estimated variances of the fitted parameters and
which have been used hereafter to compute the error bars
on . Two typical samples of the fits are shown in Figure
2. In general, the fit is good. This means that the
theoretical angular response of the antenna accounts well for the observed
spin modulation.
Finally, the systematic fits giving the , at the frequencies
explored
by Ulysses for 77 available spectra, result in 55 experimental dispersion
curves with their error boxes
(the error bars on the ratio 
correspond to the full bandwidth used to deduce each
; it is thus the range of frequencies swept
by the Ulysses receiver during half a spin).
We show on Figure 4 eight samples of such dispersion curves spread from
15 to 17 UT. Note that we have access to the second intraharmonic band only
after 
1620 UT, that is, for about half of the spectra.
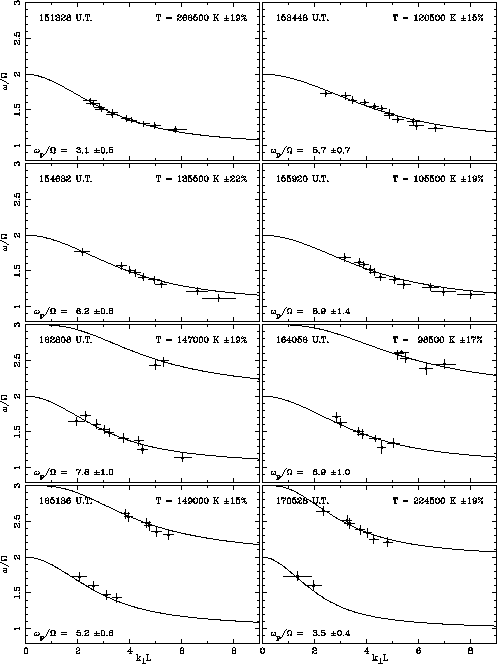
Figure 4: Eight samples of experimental dispersion curves. The points with
error bars are deduced from the observed spectra (two of them are
shown in Figure 2) and the solid line is the best fitted
solution of Bernstein's waves dispersion equation with the corresponding
electron temperature indicated on the right top of each panel.
The value of 
and 
were deduced independently by
Hoang et al., [1993]
and Meyer-Vernet et al. [1993], respectively.