The voltage power spectrum at Ulysses antenna terminals excited by such
longitudinal electrostatic waves (i.e., 
)
has been evaluated in [Meyer-Vernet, Hoang and Moncuquet, 1993] as
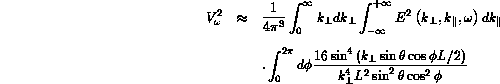
where
is the electric field power spectrum (assumed small for 
), 
(modulo 
) is the angle between the antenna
and 
(assumed not to be too close to zero), and 
is the azimuthal
angle of 
in a plane perpendicular to . We also assume a
gyrotropic distribution of waves (i.e., independent of ).
The function 
is thus the response function of a
two-wire filamental antenna (each of length L) to gyrotropic waves such that
and can be
written in the following form:
where 
and 
denote Bessel functions of the first kind.
Since we assume that the noise between gyroharmonics is due to a weakly
damped mode, that is, to a nearly real solution of the dispersion equation, one may
approximate by a delta function in the plasma dielectric function
[Sentman, 1982]. If the solution
of the dispersion equation
is unique, will be a delta function in . Indeed the
fluctuation spectrum 
of true
(undamped) Bernstein waves in a Maxwellian plasma is a delta function in
for bands below the upper hybrid frequency, because there is a
unique solution of the dispersion equation (B1) at a given frequency
(see Figure B1 in appendix B). For small 
and
bands below 
, we
assume that 
also has a unique simple zero at a given frequency,
and one sees from (1) that the spectral density varies in
this case with the angle as
where is the solution of the dispersion equation for 
.
