


Next: 4. THE STATISTICAL RATE
Up: 3. MODELING A REALISTIC
Previous: 3.2.2 Smoothing the occultation
From the previous discussion, it appears that the diffraction effect during a
stellar occultation by a KBO (and more generally by any small object
in the Solar System) will depend as usual on its size and on the
apparent distance from the star to the object (the impact parameter), but also
strongly on the apparent stellar radius and on the Fresnel scale -that means (i)
that the star has to be well selected to optimize its apparent size and flux
at the observed wavelength 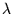 , and (ii) that such observations will
generally need another means of estimating the distance D of the occulting object
we are dealing with. We will return later to these two points, but, if we
assume these observational parameters have been fixed, the ability to
detect or not detect an object of a given size will then only depend on the
photometric precision of the instrument.
, and (ii) that such observations will
generally need another means of estimating the distance D of the occulting object
we are dealing with. We will return later to these two points, but, if we
assume these observational parameters have been fixed, the ability to
detect or not detect an object of a given size will then only depend on the
photometric precision of the instrument.
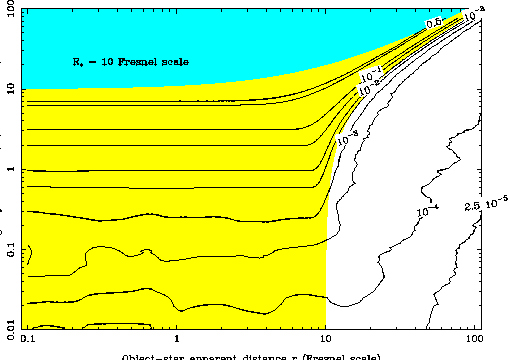
To show this dependence in the most general way possible, the
figures 3a to 3e gives the iso-levels of fluctuation, that is the maximum
amplitude of the fluctuation of the stellar intensity, as a function of the
real radius of the object and of the distance from the star to its center, both
expressed in Fsu (and both on logarithmic scale). Each figure corresponds to a
given apparent stellar radius (i.e. when projected in the occulting object plane)
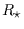 , which is 1/10, 1/2, 1, 2 and 10 Fsu, respectively.
On each figure, the
colored zones correspond to the geometric shadow: the blue zone is the complete
occultation zone and the yellow one is the partial occultation zone.
, which is 1/10, 1/2, 1, 2 and 10 Fsu, respectively.
On each figure, the
colored zones correspond to the geometric shadow: the blue zone is the complete
occultation zone and the yellow one is the partial occultation zone.
Figure 3a:
Isocontours of the maximum amplitude variation of the normalized
flux of a star occulted by an object, as a function of the distance from the
line of sight to the KBO center (horizontal axis) and of the real object
radius (vertical axis). The four non-labeled thin contours are the
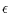 -isolevels for
-isolevels for
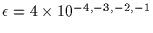 .
The grey zones correspond to the solution from geometric optics: the blue
zone corresponds
to a complete occultation and the yellow one corresponds to a partial
occultation.
This figure was computed with a ``small sized'' star, that is with an
apparent star radius of
.
The grey zones correspond to the solution from geometric optics: the blue
zone corresponds
to a complete occultation and the yellow one corresponds to a partial
occultation.
This figure was computed with a ``small sized'' star, that is with an
apparent star radius of
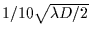 .
.
 |
Figure 3b:
As in Fig.3a, but with an apparent stellar radius of
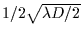 .
.
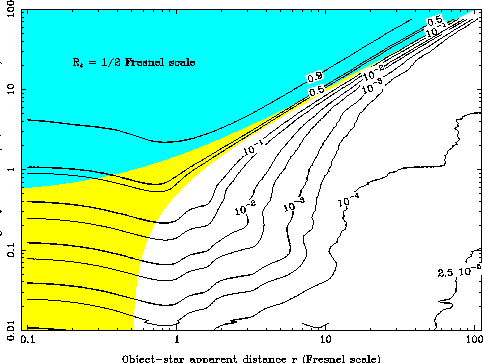 |
Figure 3c:
As in Fig.3a, but with an apparent stellar radius of
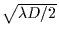 .
.
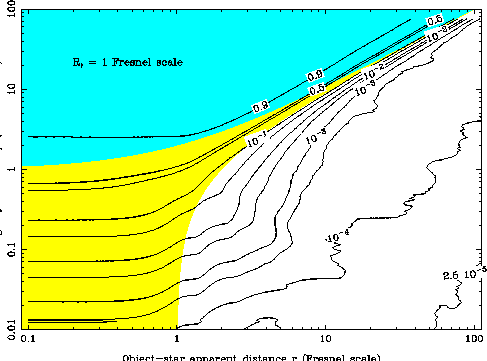 |
Figure 3d:
As in Fig.3a, but with an apparent stellar radius of
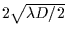 .
.
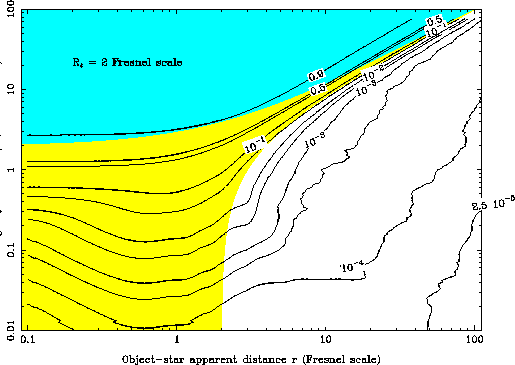 |
Figure 3e:
As in Fig.3a, but with an apparent stellar radius of
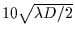 .
.
 |
Using these Fig.3a-e, we may now define the diffraction shadow for a given
sensitivity 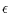 as the region where the diffraction fringes can be
detected:
as the region where the diffraction fringes can be
detected:
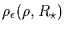 will denote the radius of the diffraction
shadow of a given object (called ``diffraction radius'' hereinafter), which
can be seen as the ``occultation effective radius'' of the object for a given
star and a given photometric sensitivity. That is, on each figure,
the isocontour of level
will denote the radius of the diffraction
shadow of a given object (called ``diffraction radius'' hereinafter), which
can be seen as the ``occultation effective radius'' of the object for a given
star and a given photometric sensitivity. That is, on each figure,
the isocontour of level  simply yields the diffraction radius
simply yields the diffraction radius
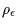 as a function of the real radius object
as a function of the real radius object 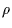 . Finally, let
us note that the Fig.3a-3e also yield the smallest detectable object
. Finally, let
us note that the Fig.3a-3e also yield the smallest detectable object
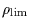 for a given star radius
for a given star radius 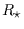 and a given sensitivity
and a given sensitivity
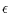 : it is the minimum reached by an isocontour of level
: it is the minimum reached by an isocontour of level 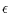 .
.
Two points must be outlined from Fig.3a-3e since they will have
important consequences on the KBOs occultation rate computation, and
more generally on photometric observations of stars in the ecliptic:
- The diffraction shadow is generally much larger than the geometric
shadow, and this ``shadow broadening'' is more pronounced as the
apparent stellar disk size decreases
and as the photometric sensitivity increases. Moreover, one can see in
figures 3a-e that the broadening due to diffraction is about a factor
1000 around or slightly below the
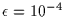 isocontour:
that means, by comparison with
the
isocontour:
that means, by comparison with
the 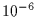 KB optical depth estimated in section 2 (assuming a density given
by Eq.4), that all the stars of the Ecliptic could have their light perturbed
at an amplitude level within the range
KB optical depth estimated in section 2 (assuming a density given
by Eq.4), that all the stars of the Ecliptic could have their light perturbed
at an amplitude level within the range
![$\sim [10^{-5},10^{-4}]$](img112.gif) .
Although such a fluctuation level is of the order of those due to star seismic
pulsations, it should not perturb the seismological observations: each
occultation event is brief (typically less than one second), so that it
involves frequencies
.
Although such a fluctuation level is of the order of those due to star seismic
pulsations, it should not perturb the seismological observations: each
occultation event is brief (typically less than one second), so that it
involves frequencies
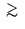 1Hz, compared to frzquencies of a mHz and below
typical of asteroseismology.
1Hz, compared to frzquencies of a mHz and below
typical of asteroseismology.
- The apparent stellar radius,
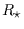 , is a critical parameter, essentially
because the occultation lightcurve is smoothed on the stellar disk, and this
smoothing effect drastically increases the size of the smallest detectable
objects (see Table I), while it generally reduces the diffraction radius:
For a 1 Fsu object radius and a
, is a critical parameter, essentially
because the occultation lightcurve is smoothed on the stellar disk, and this
smoothing effect drastically increases the size of the smallest detectable
objects (see Table I), while it generally reduces the diffraction radius:
For a 1 Fsu object radius and a 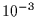 photometric sensitivity,
photometric sensitivity,
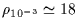 Fsu for a quasi-point star,
Fsu for a quasi-point star,
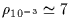 Fsu for a 1 Fsu star apparent radius, and
Fsu for a 1 Fsu star apparent radius, and
 Fsu for a 10
Fsu star, since in this case, the light fluctuation reduces to a
decrease of
Fsu for a 10
Fsu star, since in this case, the light fluctuation reduces to a
decrease of
 (as in Eq.6) due to the simple transit of the object
over the stellar disk (that is the geometric partial occultation
of the star).
(as in Eq.6) due to the simple transit of the object
over the stellar disk (that is the geometric partial occultation
of the star).



Next: 4. THE STATISTICAL RATE
Up: 3. MODELING A REALISTIC
Previous: 3.2.2 Smoothing the occultation
DESPA, Observatoire de Paris
2000-04-05
![]() , which is 1/10, 1/2, 1, 2 and 10 Fsu, respectively.
On each figure, the
colored zones correspond to the geometric shadow: the blue zone is the complete
occultation zone and the yellow one is the partial occultation zone.
, which is 1/10, 1/2, 1, 2 and 10 Fsu, respectively.
On each figure, the
colored zones correspond to the geometric shadow: the blue zone is the complete
occultation zone and the yellow one is the partial occultation zone.

![]() as the region where the diffraction fringes can be
detected:
as the region where the diffraction fringes can be
detected:
![]() will denote the radius of the diffraction
shadow of a given object (called ``diffraction radius'' hereinafter), which
can be seen as the ``occultation effective radius'' of the object for a given
star and a given photometric sensitivity. That is, on each figure,
the isocontour of level
will denote the radius of the diffraction
shadow of a given object (called ``diffraction radius'' hereinafter), which
can be seen as the ``occultation effective radius'' of the object for a given
star and a given photometric sensitivity. That is, on each figure,
the isocontour of level ![]() simply yields the diffraction radius
simply yields the diffraction radius
![]() as a function of the real radius object
as a function of the real radius object ![]() . Finally, let
us note that the Fig.3a-3e also yield the smallest detectable object
. Finally, let
us note that the Fig.3a-3e also yield the smallest detectable object
![]() for a given star radius
for a given star radius ![]() and a given sensitivity
and a given sensitivity
![]() : it is the minimum reached by an isocontour of level
: it is the minimum reached by an isocontour of level ![]() .
.