Lorsqu'une antenne électrique est immergée dans un plasma
stable, le mouvement d'agitation thermique des particules chargées produit
des fluctuations de la tension mesurée aux bornes de l'antenne. Ce bruit
(quasi)-thermique peut être calculé formellement en fonction de la
distribution de vitesses des particules et de la géométrie de
l'antenne [Meyer-Vernet and Perche, 1989]. Inversement, la spectroscopie de ce
bruit peut être utilisée pour remonter aux paramètres physiques du plasma
(voir annexe A.2).
Bien entendu, il existe des configurations
plus ou moins favorables
pour que
«ça marche», dépendantes à la fois
du plasma et de l'antenne (par exemple, ça marche
remarquablement bien avec Ulysse/URAP dans le vent solaire, voir annexe A.2).
De toutes façons, exploitable ou pas, ce bruit thermique est un phénomène
incontournable qui sera rencontré par toute expérience radio
(suffisamment sensible) qui se promène dans un plasma.
En présence d'un fort champ magnétique cependant, le bruit thermique devient assez difficile (c'est un euphémisme) à calculer, même pour une simple distribution maxwellienne des vitesses (c'est-à-dire pour un plasma à l'équilibre) et les tentatives faites prennent seulement en compte les contributions de modes particuliers [Sentman, 1982, ,] et négligent la géométrie d'antenne. Nous ne disposons donc pas actuellement d'un profil théorique de bruit thermique en plasma magnétisé pour modéliser les mesures d'Ulysse dans le tore de plasma d'Io comme on en dispose dans le vent solaire.
Avant l'analyse détaillée des spectres présentée ici, le seul diagnostic
possible se limitait à la fréquence plasma
( 
sur la figure i.4) dans la partie la plus dense du tore.
En effet, malgré l'absence d'un calcul précis du bruit thermique, on peut
utiliser le pic de densité spectrale attendu aux fréquences de
résonances «habituelles» des ondes électrostatiques, qui peuvent être, en
présence de champ magnétique, la fréquence plasma et/ou la fréquence
hybride-haute et/ou la première fréquence 
des modes de Bernstein
[Belmont, 1981, par ex.,]. Or ces fréquences sont très proches si la fréquence
gyromagnétique est petite devant la fréquence plasma(d'où la restriction du diagnostic à la partie du tore la
plus dense).
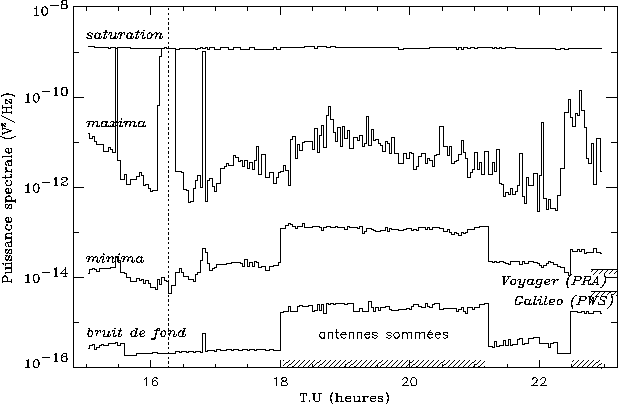
Figure i.5:
Minima et maxima (de la gyrofréquence à 48 kHz) des spectres URAP acquis
lors de la traversée du tore. Les courbes basse et haute montre
le bruit de fond de l'instrument (à la fréquence de chaque minimum) et
le niveau de saturation, respectivement. Nous avons indiqué pour comparaison
les bruits de fond instrumentaux de PRA sur Voyager 1, et de PWS sur Galileo.
La ligne verticale pointillée indique l'équateur magnétique.
À supposer qu'on dispose d'un modèle de bruit thermique
en milieu magnétisé, rien n'indiquait a priori
qu'on pourrait «voir» ce bruit
sur les spectres acquis dans le tore d'Io, en particulier si celui-ci
s'avérait négligeable à côté d'émissions en tous genres,
dues par exemple à des instabilités liées à des distributions d'énergie très
«exotiques», et susceptibles de complètement masquer ce bruit.
Or, il n'en a rien été, et un point-clé de l'analyse du
spectrogramme basses-fréquences de la
fig.i.4 est la remarquable stabilité
de la densité spectrale pendant ces 9 heures d'observations.
On montre cette stabilité sur la figure i.5 où sont représentées les
valeurs extrêmes atteintes par le signal en fonction du temps :
d'une part, les minima
du signal restent à un niveau très stable
(excepté les nettes variations due à l'addition
du signal de l'antenne Z durant les périodes indiquées par des hachures).
Cette stabilité n'est pas un effet de seuil de sensibilité,
car ces minima sont mesurés
largement au-dessus du bruit de fond de l'instrument.
D'autre part, les maxima atteints sont restés aussi à un niveau assez stable
(l'instrument n'a saturé que pour quelques spectres au voisinage de
l'équateur magnétique).
Il serait très surprenant que des instabilités aient fourni pendant neuf heures la
puissance idoine pour maintenir l'amplitude absolue du signal
collecté d'un spectre à l'autre à un niveau aussi stable!
Outre la stabilité des extrema de la puissance spectrale, ceux-ci sont mesurés à des fréquences bien particulières : comme on le voit sur la figure i.6, les minima (absolus) sont très majoritairement placés sur les harmoniques de la gyrofréquence et les maxima (absolus) se trouvent à mi-chemin entre celles-ci.
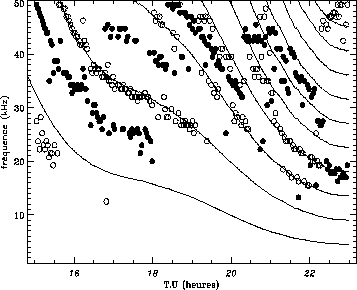
Figure i.6: Fréquences des minima absolus (cercles)
et des maxima absolus (points) du spectre dynamique I.4 . On a tracé
la fréquence gyromagnétique et quelques-unes de ses harmoniques.
Plus généralement, comme on l'a déjà remarqué sur le spectre BF de la
fig.i.4, les spectres présentent tous une modulation en rapport
étroit avec le mouvement cyclotron des électrons : ils atteignent
des minima relatifs aux fréquences gyroharmoniques
et présentent un accroissement (modéré) de densité spectrale entre chacune de
ces fréquences. L'interprétation s'impose naturellement :
le bruit qui «surnage» au-dessus du bruit minimum mesuré par l'antenne,
entre les fréquences gyroharmoniques, doit être dû aux ondes électrostatiques
entretenues par le mouvement cyclotron des électrons, autrement dit les modes
de Bernstein (qui sont, par définition, des ondes électrostatiques
propageant perpendiculairement au champ magnétique). Ces modes propagent
sans amortissement entre les harmoniques de la fréquence gyromagnétique
, ce qui en fait des candidats de choix pour expliquer
l'accroissement du signal entre ces harmoniques mais il convient d'y regarder
d'un peu plus près concernant les conditions d'amortissement des ondes dans
un plasma magnétisé.
Rappelons qu'une condition générale pour des électrons
de vitesse moyenne
d'amortir (ou d'exciter)
une onde 
est [Stix, 1992, voir par ex. p270,]:
(n est un nombre entier),
ce qui n'exprime rien
d'autre que l'égalité entre la fréquence de l'onde et celle de l'oscillateur
formé par les électrons dans leur gyration autour des lignes de champ,
compte-tenu du décalage Doppler dû à leur mouvement le long des lignes de champ.
Si on considère une distribution des vitesses à deux populations froide et
chaude (core + halo), cette condition d'amortissement explique pourquoi on ne
voit entre les gyroharmoniques que les modes dont le 
est
suffisamment petit pour qu'ils ne soient pas amortis par le gros des électrons
(les froids), ce qui nécessite effectivement 
petit devant
. Ceci explique aussi pourquoi l'augmentation du signal
entre les gyroharmoniques sera contrôlée par la population chaude (ou halo) des
électrons. Notons qu'exactement à la fréquence gyromagnétique
(ou à une de ses harmoniques)
ce non-amortissement gradué par les chauds disparaît et le bruit est minimum,
correspondant au bruit
thermique «sans mode de Bernstein», produit essentiellement par
les électrons froids.
Les explications qui précèdent sont purement qualitatives et n'ont d'autre but que de montrer la démarche heuristique qui a prévalu pour analyser ces spectres d'Ulysse. On a en particulier omis de parler de la partie «antenne», qui va favoriser ou atténuer tels ou tels modes. On trouvera les calculs détaillés quantifiant le raisonnement «sur le coin de la table» précédent (et tenant compte de la réponse d'antenne) dans [Meyer-Vernet, Hoang and Moncuquet, 1993] et dans les deux articles présentés au chapitre suivant. Les résultats de ces calculs comparés aux mesures d'Ulysse sont autant de vérifications de l'auto-cohérence de notre interprétation; à cet égard, on peut citer :
1) l'élévation du niveau de bruit observée entre les gyroharmoniques est celle
obtenue par le calcul en mode de Bernstein [Meyer-Vernet, Hoang and Moncuquet, 1993]
pour une population d'électrons
chauds telle que celle observée sur
Voyager 1 par [Sittler and Strobel, 1987]
2) La modulation due à la rotation de l'antenne dans le champ magnétique est
celle attendue pour les modes de Bernstein (le signal est maximum
quand l'antenne est parallèle à 
pour des longueurs d'onde
petites devant la longueur de l'antenne), et est l'opposé de ce qu'on
attend pour des ondes (de Langmuir) propageant parallèlement à .
3) Les courbes de dispersion obtenues expérimentalement
à partir des spectres d'Ulysse (voir ici ) sont très semblables aux
courbes de dispersion théoriques des modes de Bernstein.
4) Le niveau minimal du bruit observé aux gyroharmoniques est bien
celui que l'on calcule
avec les densités déterminées dans [Hoang et al., 1993] et les températures des
froids déterminées dans
[Moncuquet, Meyer-Vernet and Hoang, 1995] (déterminations indépendantes bien sûr de ce niveau).
Notons pour finir ce chapitre que notre analyse de
ces «bandes» de bruit entre les
gyroharmoniques observées par Ulysse montre que celles-ci
ne sont pas dues à des instabilités du plasma;
cela est aussi vrai pour les bandes
de bruit observées dans le tore avec Voyager 1 par [Birmingham et al., 1981]
(ce qui avait d'ailleurs été suggéré par [Couturier et al., 1981] et
vérifié par [Sentman, 1982]). Il en va généralement de même,
contrairement à ce qui est souvent affirmé avec aplomb, des émissions dites
« 
» observées dans d'autres magnétosphères.