Sur Voyager 1, les expérimentateurs ont ajusté aux mesures de distributions,
en particulier pour
les électrons, un modèle de distribution de type «coeur + halo»
[Sittler and Strobel, 1987], 
c'est-à-dire
un modèle obtenu en additionnant deux maxwelliennes de température et de
densité différentes. Le résultat est néanmoins une distribution de facto
non-maxwellienne et on peut donc se demander si ce choix de distribution permet de
prévoir un gradient de température le long des lignes de champ et
éventuellement un indice polytrope.
Soit donc une distribution définie par la somme de deux distributions
maxwelliennes de densités 
et de températures 
,
correspondant respectivement à la maxwellienne du coeur(froid) et du
halo(chaud). Avec une telle distribution, on peut définir la température
maxwellienne traditionnelle 
et la
température effective : 
. Pour
simplifier l'écriture, on pose : 
et 
(avec
par conséquent 
et 
, les limites de ces domaines
ramenant dans tous les cas la distribution à une simple maxwellienne) et on
exprime la filtration des vitesses en considérant que la densité des froids
à l'équateur va être multipliée par un facteur
à l'altitude s. On obtient la variation des
températures avec la latitude pour ce type de distribution coeur + halo :
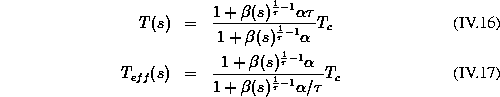
Pour Voyager 1, à cette distance de 
, on avait 
et 
, et donc si ces conditions étaient réalisées au passage
d'Ulysse, les équations précédentes permettent de prévoir, par exemple à une
latitude où la densité des froids est divisée par 4 (i.e. 
), une
variation de T d'environ 50%, une variation de 
d'environ 5%
(alors que la température effectivement mesurée par Ulysse double lorsque
est divisée par 4) .
Remarquons pour finir cette petite digression, qu'avec ce type de distribution
coeur+halo, la loi polytrope qu'on pourrait dégager serait, vu ce qui précède,
dépendante de la température considérée, et donc de la sensibilité de la
mesure à tel ou tel moment de la distribution, c'est-à-dire
en définitive dépendante de l'instrument utilisé.