Retour aux -distributions

À ce stade de l'analyse, nous avons donné une interprétation qualitative (filtration des vitesses sur une distribution non-maxwellienne) et quantitative (filtration sur une -distribution) de la surprenante augmentation de la température des électrons froids avec la latitude mesurée par Ulysse, ainsi que de la loi polytrope à observée. Néanmoins, l'étape suivante, qui consiste à calculer le profil de densité le long d'une ligne de champ, ou en d'autres termes le confinement du tore, qui devrait être a priori différent de celui obtenu avec les modèles disponibles, n'est pas encore accessible puisque l'équation iv.13, lorsqu'on l'écrit pour les électrons, dépend du potentiel de confinement des électrons du tore qui nous est inconnu.

En introduisant la notion d'équateur centrifuge (chapitre i, section i.1.1), on a ébauché le calcul de la composante parallèle au champ magnétique de la force mécanique centrifuge due à la corotation du plasma. Cette force, qui dérive d'un potentiel, est proportionnelle à la masse de la particule considérée et est par conséquent une composante déterminante du mouvement des ions (au minimum 1800 fois plus massifs que les électrons) le long des lignes de champ. Comme le plasma doit rester électriquement neutre, il faut, d'un point de vue microscopique, que les électrons subissent une force électromotrice appropriée pour «suivre» le mouvement des ions, ce qu'on modélise macroscopiquement par l'introduction d'un champ électrique ambipolaire parallèle au champ magnétique de Jupiter, changeant de signe à l'équateur centrifuge et dérivant d'un potentiel électrostatique (noté par la suite ) négatif (pour confiner les charges négatives). En première approximation (on raffinera dans le chapitre suivant), le potentiel électrique ambipolaire confinera donc les électrons autour de l'équateur centrifuge, tout comme seront confinés les ions du plasma par le potentiel centrifuge + le potentiel (où Z désigne le nombre de charge d'un ion).

On voit ainsi que ce potentiel , nécessaire pour calculer le profil de densité des électrons, dépend fondamentalement des ions (via l'équation de neutralité du plasma), et par conséquent de leurs distributions de vitesses, mais aussi de leurs natures chimiques et de leurs proportions respectives dans le tore, c'est-à-dire globalement d'un modèle de composition physico-chimique du tore de plasma d'Io (toutes choses dont nous ne pouvons hélas pas disposer avec Ulysse). La construction d'un tel modèle, élargi à des distributions kappa anisotropes des ions et pour les différentes espèces d'ions détectées dans le tore par Voyager 1 (c'est-à-dire généralisant aux distributions kappa anisotropes le modèle construit par Mme Bagenal en utilisant des distributions bi-maxwelliennes) fait justement l'objet du reste de la thèse (chapitres v et vi).

Pour clore ce chapitre, je veux présenter ici brièvement le premier modèle de tore de plasma d'Io fondé sur une distribution kappa, que nous avons proposé dans l'article de Meyer-Vernet, Moncuquet and Hoang, [1995] reproduit en annexe B.1. Ce modèle permet d'obtenir un profil de densité électronique en fonction de la latitude centrifuge en faisant des hypothèses simples (mais non simplistes), en particulier sur la distribution des ions et leur composition. J'en résume ici le principe et les résultats fondamentaux, et j'invite le lecteur à se reporter pour plus de détails à la section 5 de l'article [B.1] :

Si l'on suppose que les ions en présence sont formés d'une seule espèce (hypothèse simplificatrice, nous l'admettons, qui sera levée dans le chapitre suivant) et que leur distribution de vitesse est une -distribution (c'est une hypothèse de construction défendable et effectivement défendue dans le chapitre suivant) dont le est identique à celui des électrons (c'est l'hypothèse la plus arbitraire, et n'a d'autre justification que de rendre possible un calcul analytique, mais elle sera aussi levée dans les chapitres suivants) alors on peut écrire l'équation iv.13 pour les électrons et les ions en y ajoutant la neutralité du plasma quelque soit la latitude : [voir Éq.(22) de B.1]. On obtient un profil de densité qui a la forme d'une Lorentzienne généralisée en s :

 

où H est une échelle de hauteur caractéristique de ce profil, analogue à l'échelle de hauteur d'un modèle gaussien [Bagenal and Sullivan, 1981, Divine and Garrett, 1983, Hoang et al., 1993] que l'on aurait obtenue en utilisant une distribution maxwellienne (avec les mêmes hypothèses simplificatrices).

On déduit aussi, en utilisant une forme simplifiée du potentiel centrifuge, une expression de H en fonction de la température des ions et des électrons à l'équateur centrifuge [voir Éq.(24)&(25) de B.1]. Notons qu'on peut aussi déduire ce profil de densité iv.18 en utilisant une description fluide du plasma, et en supposant vérifiée au préalable une loi d'état polytrope entre n et T à . On obtient alors un profil de densité comparable à celui de iv.18 mais exprimé en fonction de l'indice polytrope , de telle sorte que cet indice soit relié au de iv.18 par l'équation iv.15. On montre ensuite dans cet article [B.1] qu'on peut déduire l'échelle de hauteur H en ajustant (au moindre ) le profil de densité iv.18 au profil mesuré par Ulysse. On obtient un ajustement assez bon ( ) pour une échelle de hauteur . Ce modèle simple a été récemment utilisé par [Thomas and Lichtenberg, 1997] pour interpréter des profils de température dans le tore d'Io (déduites d'observation en infrarouge depuis la Terre).

On a représenté dans un plan méridien sur la figure iv.3 entre 7 et (là où l'on a observé la loi polytrope et donc «validé» le des électrons) un «modèle 2-D» calculé avec le profil «kappa-like» donné en iv.18, et le gradient de densité à l'équateur centrifuge de Voyager 1. On a représenté pour comparaison un modèle de densité électronique déduit de [Bagenal, 1994] (supposé isotrope, champ ) à l'extérieur du domaine de validité de notre loi polytrope.

Au vu de ce type de comparaison, on a pu déclarer [Stone et al., 1992b], y compris nous-mêmes [Hoang et al., 1993, dans ,], qu'à l'époque de la rencontre Ulysse-Jupiter (1992), on avait vu un tore deux fois plus dense à l'équateur et beaucoup plus confiné autour de l'équateur centrifuge . Il faut à présent relativiser ces affirmations parce qu'elles sont fondées sur une comparaison entre de vraies mesures en latitude (pour Ulysse) et une extrapolation en latitude des mesures de Voyager 1, fondée sur des hypothèses (équilibre thermique local) qu'on a trouvées définitivement incompatibles avec les mesures de température d'Ulysse (voir tout ce qui précède).

  
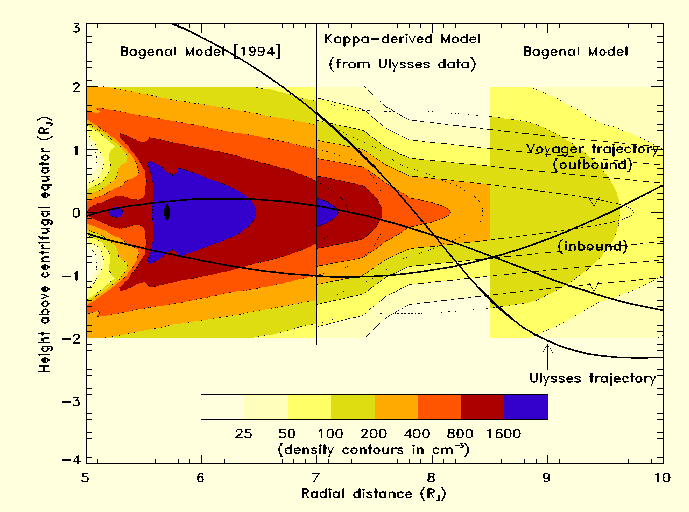
Figure iv.3: Un modèle simplifié de densité électronique limité au domaine exploré utilement par Ulysse dans le tore de plasma d'Io et calculé à partir d'une -distribution isotrope ( ) pour toutes les particules. Le profil en altitude s est une fonction Lorentzienne en s d'échelle de hauteur . Le gradient de densité électronique utilisé à l'équateur centrifuge est celui de Voyager 1 (mais la densité absolue est multipliée par 1.9 pour s'ajuster à celle mesurée par Ulysse).(Figure extraite de Moncuquet [1995])

Il est à cet égard amusant de constater qu'au point commun en latitude et distance jovicentrique des trajectoires d'Ulysse et de Voyager 1 (immersion) (voir cette intersection sur la figure iv.3) les densités électroniques mesurées par les deux sondes à 12 années d'intervalle sont très semblables (à quelques % près pour une densité d'environ 300cm ).