Equation (1) shows that the 
frequencies are independent on the core
temperature 
. To show how the other parameters of the distribution affect
the solutions of the dispersion equation and thus the determination of the
plasma frequency from the 
, we have plotted
(Figure 3) a set
of dispersion curves with 
(and therefore 
) held constant and
the suprathermal electron parameters values chosen in the wide ranges:
and 
.
One can see on Figure 3 that the
largest Doppler-shifted Q resonance in each band is never the 
and that
is nearly independent of the sampled halo parameters, so that the
forbidden band lower limit that we detect is only a function of .
We can
then determine by fitting the calculated to the frequency
at which the signal plummets (as shown in Figures 2a and 2b (bottom));
as long as the halo parameters remain in the above ranges, our method yields
the core population density.
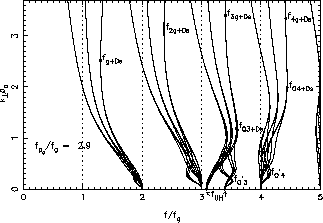
Figure 3: Examples of dispersion curves for four halo
velocity distributions: 
or 0.25 and 
or 50;
is constant. The symbols have the same meaning as in Figure 1.
The 
,
which are linked to the
hot population, always arise (in the sampled parameters
range) below the , which is roughly independent on the hot
population (as the 
).