

Next: 2.2. Computing the Antenna
Up: 2. From Measured Spectra
Previous: 2. From Measured Spectra
In order to interpret the spectral density observed, let us
emphasize two observational facts:
1. The signal is extremely
stable. It has no growing peak or saturation (except in the close vicinity
of the magnetic equator), and the variations of the
midband amplitude and spectral shape are very small and smooth
during the several hours duration of the IPT encounter
(Figure 1).
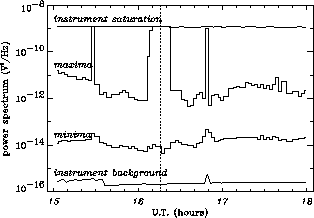
Figure 1: Absolute minima and maxima (from the
gyrofrequency to 48.5 kHz) for each of the 77 power spectra acquired by
Ulysses during its Io torus crossing on February 8, 1992 (of which two
examples are shown in Figure 2). Except in the few cases
where the instrument was saturated, six cases close to the magnetic equator
(which is indicated as a dotted line) and two isolated cases, the ratio
between the maxima (which take place roughly in the middle of the
gyroharmonic band) and the minima (which are always very close to
a gyroharmonic) is about two decades.
The bottom and top curves
show the instrument noise level at the frequency of each minimum
and the instrument saturation level at
the frequency of each maximum, respectively.
This signal can be quantitatively interpreted as
quasi-thermal noise from suprathermal electrons
[Meyer-Vernet, Hoang and Moncuquet, 1993]. The lack of variation in the
signal's intensity over time suggests the kind of configuration the ambient
plasma is in; here
we mean that the distribution may be multi-Maxwellian or
kappa-like but does not contain beams, loss cones, or other strong
anisotropic features with enough free energy to drive instabilities.
It is indeed difficult to imagine that an unstable distribution
(see for example [Kennel and Ashour-Abdalla, 1982]) could
yield the roughly constant midband amplitudes observed during more than
3 hours (see Figure 1) at a level which is just what is expected
from the (stable) 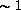 keV suprathermal component present in this
region [Sittler and Strobel, 1987].
This point will be confirmed by
our experimentally derived dispersion curves in the next section.
keV suprathermal component present in this
region [Sittler and Strobel, 1987].
This point will be confirmed by
our experimentally derived dispersion curves in the next section.
2. The power into the antenna reaches its lowest level, the thermal level,
at gyroharmonic frequencies. The signal
increases smoothly to about a hundred times that value in the middle of the harmonic
bands (see Figure 1 and two samples on Figure 2). Here
we shall not calculate explicitly the amplitude between the gyroharmonics,
since that would involve an arbitrary chosen velocity distribution
[Sentman, 1982];
but we may remark that a general condition for electrons of
velocity  to damp (or excite) a wave
to damp (or excite) a wave 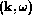 in a
magnetized plasma is just
in a
magnetized plasma is just
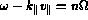 ,
where n is an integer,
,
where n is an integer,
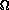 is the angular gyrofrequency, and
is the angular gyrofrequency, and 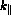 and
and 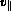 denote parallel projections
of
denote parallel projections
of 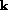 and
and  , respectively, on the magnetic field
, respectively, on the magnetic field 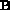 .
This equation only expresses the equality between the wave
frequency and the frequency
of the oscillators formed by the electrons spiraling along
the magnetic field, taking into account the Doppler shift
due to the velocity parallel to
.
This equation only expresses the equality between the wave
frequency and the frequency
of the oscillators formed by the electrons spiraling along
the magnetic field, taking into account the Doppler shift
due to the velocity parallel to 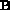 .
Hence all waves with
.
Hence all waves with 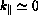 are damped at gyroharmonic
frequencies and weakly damped between them, and we may assume that the
signal enhancement between gyroharmonics is due to the excitation of such
waves by suprathermal electrons. For these electrons,
are damped at gyroharmonic
frequencies and weakly damped between them, and we may assume that the
signal enhancement between gyroharmonics is due to the excitation of such
waves by suprathermal electrons. For these electrons,
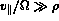 (the thermal electron gyroradius), and if
(the thermal electron gyroradius), and if
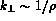 (as we shall see), the condition
(as we shall see), the condition 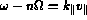 can thus only be met between gyroharmonics for
can thus only be met between gyroharmonics for
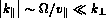 .
.


Next: 2.2. Computing the Antenna
Up: 2. From Measured Spectra
Previous: 2. From Measured Spectra
Michel Moncuquet
Tue Nov 18 19:18:28 MET 1997
