Tout écart aux conditions énoncées au début (champ magnétique statique uniforme
et pas de forces extérieures) provoque, outre la variation de 
déjà décrite, l'apparition d'une vitesse de dérive perpendiculaire aux
lignes de champ et qui se superpose à la vitesse 
du mouvement
cyclotron 
.
Par exemple, un champ magnétique planétaire poloïdal provoquera
l'apparition d'une vitesse de dérive due à la courbure de ses lignes de champ et
d'une vitesse de dérive due au gradient de sa magnitude. On montre
aussi que la présence d'un champ de force 
(par exemple de pesanteur)
agissant sur la particule produit une vitesse de dérive donnée par
. Si 
varie dans les limites de validité de l'approximation
adiabatique , ces vitesses de dérive sont faibles devant celles
du mouvement quasi-hélicoïdal.
En revanche, dans le cas de la magnétosphère d'une planète possédant un champ
poloïdal, il existe une variation forte (non adiabatique) mais régulière du
champ magnétique, due à la rotation de la planète
qui entraîne avec elle les pôles et les lignes de forces de . Cette
rotation du champ se traduit, via le «gel» du champ magnétique dans le plasma,
par l'entraînement du plasma avec la rotation planétaire.
Montrons brièvement qu'on peut voir cet effet en terme de vitesse de dérive;
considérons le champ électrique 
induit
par la rotation des lignes de champ dans un référentiel inertiel : il sera
responsable d'une dérive du centre guide des particules à la vitesse
. Calculons cette
vitesse de dérive: le champ électrique vu en un point P de la magnétosphère,
dans un référentiel tournant avec la planète (de centre O et de vecteur
rotation 
) à la vitesse
est alors 
.
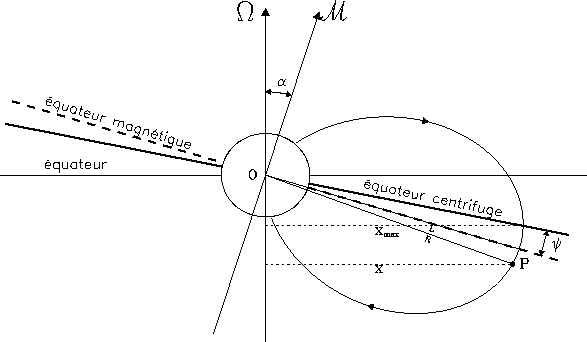
Figure i.1:
L'équateur centrifuge est ici tracé dans un plan méridien contenant l'axe du
moment magnétique 
d'un dipôle centré, incliné d'un angle
sur l'axe de rotation planétaire de vecteur . L'équateur
centrifuge est défini comme lieu des points les plus éloignés de l'axe de
rotation sur chaque ligne de champ. L'angle 
formé par l'équateur
magnétique et l'équateur centrifuge atteint son maximum dans ce plan
et vaut 
pour un angle
petit [Hill et al., 1974] (pour Jupiter, 
3.2°). Un point P de
la magnétosphère sera aisément repéré vis-à-vis du champ
magnétique par le "rayon magnétique équatorial (ou dipolaire)" L de la ligne de champ auquel il
appartient, et vis-à-vis d'un plasma en corotation (tore) par sa latitude
centrifuge (angle à l'équateur centrifuge local).
Dans l'approximation du champ magnétique «gelé» dans le plasma (fluide de
conductivité infinie), 
est nul; on a donc 
, soit, pour une particule de centre guide en P,
une dérive électrique 
(où 
désigne la
composante de 
parallèle à ). Ainsi, à une vitesse parallèle
à près, la vitesse imprimée au centre guide de la particule est égale
à la vitesse de rotation axiale rigide 
.
Autrement dit, les lignes de force du champ magnétique
entraînent dans leur rotation les particules chargées, à la vitesse de
corotation rigide 
x, où x est la distance de la particule à l'axe de
rotation de la planète [voir fig.i.1] : le plasma est dit en
corotation planétaire .
On en déduit une importante conséquence quant à la position d'équilibre des
particules sur les lignes de champ: entraînées à la vitesse de corotation
rigide, elles subissent une force centrifuge 
dont la composante
parallèle à
est une force de rappel qui s'annule sur la ligne de champ au point
le plus éloigné de l'axe de rotation planétaire (cf. x 
sur la figure
i.1), c'est-à-dire au point où est parallèle à
.
Montrons le brièvement: l'accélération centrifuge de la rotation solide
est donnée au point P par 
,
soit, en projetant dans la direction de :
est l'angle que fait le champ magnétique avec l'axe
de rotation planétaire 
.
Dans la magnétosphère de Jupiter et pour des distances de 4 à 13 
, cette
force de rappel centrifuge est, pour le gros des particules , beaucoup plus importante que la force miroir
magnétique (voir une comparaison dans [Cummings, Dessler and Hill, 1980]). Bien entendu,
cette force n'agit effectivement que sur les ions, qui ont une masse
conséquente. En ce qui concerne les électrons, bornons-nous à remarquer qu'ils
devront «suivre» les ions pour conserver la neutralité du plasma, d'où
l'apparition d'un champ électrique (dit ambipolaire) et donc d'une force
électromotrice qui jouera pour les électrons le rôle de force de rappel, mais
ce point sera développé plus en détail dans la deuxième partie de cette thèse.
C'est donc finalement cette force de rappel (ou de confinement) centrifuge qui
déterminera sur chaque ligne de champ le point d'équilibre autour duquel les
particules chargées seront effectivement confinées : ces points forment une
surface de symétrie (et de densité maximale)
du plasma en corotation, qu'on appelle équateur centrifuge.