It is well known that the electron velocity distribution in the IPT is not
fully Maxwellian [Scudder, Sittler and Bridge, 1981].
The results of the particle analyzers
aboard Voyager have been modelled by the sum of
a cold (density 
, temperature 
) and a hot (density 
,
temperature 
) Maxwellian distribution, with 
a few
percent and 
10-50 [Sittler and Strobel, 1987] at the Jovicentric distance
. In this kind of plasma, the
part of the dispersion relation used to deduce the temperature
is mostly sensitive to the main (cold) population.
This holds because we mainly consider harmonic bands of order smaller
than 
and 
of order of magnitude
unity, 
being the cold-electron gyroradius. In that case, the presence of the
hot electrons only changes the
dispersion for 
of order 1, that is, for values of k too small to
be considered here. This is illustrated in Figure 7, which shows
how small the change is in the dispersion curves, even when the hot population
represents 
of the total density.
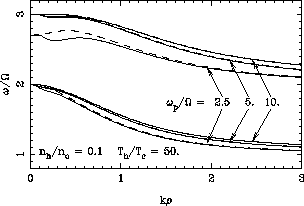
Figure 7: Dispersion characteristics of Bernstein waves for two
Maxwellian populations of electrons. The solid lines are computed using
(5) with 
in the two first
intraharmonic bands and for three typical values of encountered
by Ulysses during its torus crossing. The proportion of the hot population ( )
has been exaggerated in order to show an appreciable difference with the pure
Maxwellian case (dashed lines). The dispersion characterictics are only
modified for small 
(as explained in the text) and more significantly
when is less than the upper limit of the intraharmonic
band considered, especially for the 
determination.
The actual proportion is smaller
and introduces a change which would be barely visible on Figure 7.
Hence the temperature plotted in Figure 5 represents in this case the cold
electron temperature .
It is not certain, however, that the cold population
itself is exactly Maxwellian.
The Voyager analyzers could
only measure the electrons of energy larger than 10 eV, and owing to
the negative spacecraft charging, the actual cutoff was higher.
On the other hand, aboard Ulysses the
frequency range in which we measured the dispersion relations
is not large enough to determine whether the cold
electrons are exactly Maxwellian. For example, if we consider a
distribution made of two Maxwellians with 
and 
, the shape of the part of the dispersion
relation used in our analysis is not significantly changed, that is, k is only
changed by a roughly constant factor
(see Figure 8).
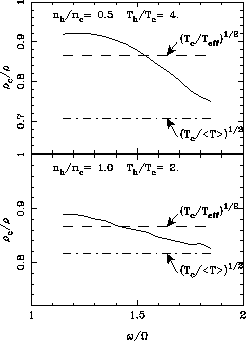
Figure 8: Ratio of the solution of the dispersion equation , with
a population made of two Maxwellians (c and h), to the solution
, with a single Maxwellian, for two values of 
and 
and 
.
For 
, the ratio remains within of
, which means that the shape of the dispersion curves is not
significantly changed and that our measurement yields the effective
temperature 
.
Near the harmonic 
, the measurement would yield the usual
temperature 
.
With such a non-Maxwellian distribution, what is the
significance of the temperature deduced from the measured
dispersion relation, that is, what is the temperature of the single
Maxwellian which would give approximately the same 
in the
measured frequency range? Bernstein's dispersion equation
generalized to a sum of Maxwellian populations reads
where 
is a modified Bessel function of the first kind and
Here 
and 
are
the parameters of each Maxwellian population
( 
) of the distribution. Now our measurements are made
mostly in the middle of the first gyroharmonic band ( 
). In this case, it is easy to see that (1) the terms
are dominant in (5) if all the densities
have
similar orders of magnitude, and (2) the parameters 
remain
of the order of unity if all the temperatures
have the same order of magnitude. In that case, one finds that
the terms 
are roughly
equal so that 
factors out of the equation.
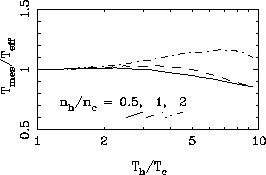
Figure 9: Comparison of the temperature 
deduced from Bernstein's
dispersion relation (near the middle of the first
gyroharmonic band, for ) to the effective temperature
(equation (6), with ) for a distribution made
of two Maxwellian populations.
Hence a sum of Maxwellians
should give approximately the same as a single
Maxwellian
having the same total density and an effective temperature given by
This can be verified by numerical computation, as shown in
Figure 9, where we have drawn the ratio of the temperature
deduced from the dispersion relation by assuming a single Maxwellian
to the effective
temperature given by (6), when the
actual distribution is the sum of two Maxwellian
populations ( ). One sees that
when the densities and temperatures of the populations
making the distribution have similar orders of magnitude or if
the hot population density is much smaller than the cold one.
(This would not hold for higher gyroharmonic
bands or close to gyroharmonics.) Note that is
not proportional to the mean square velocity (as is the usual
temperature 
) but is instead
proportional to the mean
inverse square velocity. It is thus mainly sensitive to the
cold electrons.
