During the period 
1710 to 18 UT, no measurements of the
density are available. Actually, the upper hybrid frequency 
probably falls
between the two lowest-frequency channels of the URAP high-frequency
receiver (52 and 66 kHz);
it is thus no longer possible to identify in the HF spectra
in order to deduce the density [Hoang et al., 1993].
It also could not be deduced from
the onboard particle analyzers, since they were not operational in the
IPT.
Nevertheless, we can still determine the plasma dispersion characteristics
from the spectrum modulations, since the method is independent of the plasma
density. Then, is it possible to determine both the temperature and the
density by fitting a solution of the
dispersion equation with two adjustable parameters ( 
and 
)?
A necessary condition is of course
that this solution significantly depends on the plasma frequency. Owing to
the expression of the derivative given by (B2)
(this derivative, in respect with , is plotted on Figure B1),
this condition only holds in the upper hybrid band and above. This range
includes the so-called 
frequencies at which
the wave group velocity vanishes (see upper panel in Figure B1),
and there is a frequency gap in the spectrum
of Bernstein waves between each and
the upper consecutive gyroharmonic [Bernstein, 1958].
The nondetection of the upper hybrid frequency
during the period 1710 to 18 UT, in the frequency range where the HF
receiver has sufficient frequency resolution, implies that our low-frequency
spectra indeed includes a part of that upper hybrid band, which is the band
. There are, however, two problems:
(1) the greatest dependence on
occurs in the range of small values of 
(see Figure B1),
which, as we have
seen in section 2, are difficult to measure, and
(2) our determination of k from the spin modulation only
works for frequencies where the dispersion equation has a unique solution
in k: this excludes frequencies between and .
With these limitations in mind, we tried to fit the theoretical dispersion
curves to the experimental ones using the same method as
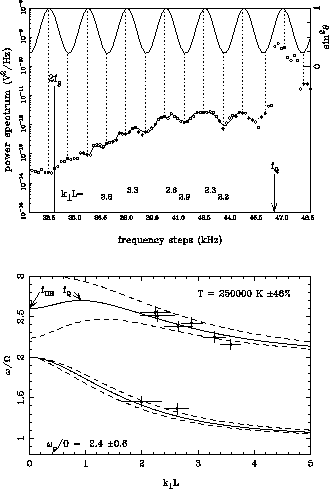
Figure 6: (top) Part of the spectrum observed at 1714 UT above the second
gyroharmonic frequency. The small circles are the measurements and the solid
lines are the best fitted antenna response with corresponding values of
indicated below. The value of is that computed
from the dispersion curves shown on the bottom panel.
(bottom) The points with error bars are deduced from
the spectrum and the solid lines are the best fitted solution of Bernstein's waves
dispersion equation with two free parameters T and . The dashed
lines are the solutions of the dispersion equation for the extrema
values of in its range of uncertainty.
before but with two adjustable parameters: the electron
gyroradius and the ratio 
.
Owing to the above limitations, and also because of the difficulty to
numerically separate the dispersion variations due to from the
variations due to , the results of these
fits are not very good. The fitting method yields acceptable least 
for
only 12 dispersion curves out of 20 available ones, and the uncertainties are about
for the temperature and 
for the density. These results are added
on Figure 5 with error bars in dotted lines.
Despite the large error bars on the density, we may remark that the ratio
probably does not fall under 
during this period;
otherwise, the would be in the range of frequencies swept by the receiver
(<48.5 kHz with a gyrofrequency about 20 kHz). In this case, one would
expect two
important qualitative changes in the observed spectra: (1) the quasi-thermal
noise should peak at and , where the group velocity
vanishes, and (2) the signal should fall
abruptly just above until the following gyroharmonic, since no weakly
damped mode exists in that band. Actually, we show in Figure 6 a
spectrum where there is a power jump in the vicinity of the (computed
from the fitted dispersion curves), which can satisfy our first statement. Owing
to the limited frequency range of the receiver, this spectrum is the only one
among the 20 available spectra in that period (before 18 UT) to show such
behavior. However, since both and 
decrease with distance to
Jupiter, the two above expected properties are routinely seen on the spectra
acquired at later times; this can be used to determine the density
(M. Moncuquet et al., manuscript in preparation, 1995).