Inversion des températures

Parmi les résultats obtenus sur Ulysse par spectroscopie du bruit quasi-thermique, décrits en détail dans la première partie (cf figure iii.2), on s'intéresse particulièrement au cas où l'on peut disposer à la fois d'une mesure de la densité et de la température des électrons, ces mesures étant acquises indépendamment l'une de l'autre.

  
Figure iv.1: Densité et température des électrons dans la partie externe du tore d'Io (le tore "chaud"), en fonction de la latitude centrifuge. [adapté de Meyer-Vernet, Moncuquet and Hoang, 1995]

On a représenté sur la figure iv.1 les densités [Hoang et al., 1993, d'après,] et les températures [Moncuquet, Meyer-Vernet and Hoang, 1995, d'après,] des électrons en fonction de la latitude centrifuge, c'est-à-dire par rapport à l'équateur physique du tore (cf i.1.1). Les barres d'erreurs indiquées en trait continu sur cette figure correspondent à des mesures obtenues par des méthodes indépendantes. La latitude centrifuge est déterminée en utilisant un modèle simplifié du champ magnétique jovien (un dipôle incliné), largement suffisant pour ce qu'on souhaite montrer ici, compte-tenu des barres d'erreurs.

Indubitablement, Les mesures des densités et températures électroniques présentées sur la figure iv.1 remettent en cause les bases de la description latitudinale du tore et de son équilibre thermodynamique : contrairement à ce que supposaient tous les modèles précédents, fondés sur l'équilibre thermique local (isotherme pour chaque espèce de particule) [[Bagenal and Sullivan, 1981]; Divine and Garrett, 1983; [Bagenal, 1994]] ) du plasma le long des lignes de champ, la température n'est pas constante lorsqu'on se déplace le long d'une ligne de champ mais est, au contraire, très significativement croissante avec la latitude centrifuge ( double sur 7° de latitude). On peut tout d'abord se demander si cette contradiction flagrante entre la mesure des températures électroniques réalisée pour la première fois en vraie grandeur (i.e. à des latitudes non négligeables) par Ulysse et l'hypothèse largement admise jusqu'ici de l'équilibre diffusif isotherme du plasma le long des lignes de champ n'est pas seulement dû à une mauvaise interprétation de nos mesures. Je distinguerai, pour y répondre d'emblée, deux mises en cause possibles, dont la deuxième est celle qui nous a mis la puce à l'oreille pour aboutir à notre propre explication.

1) l'augmentation de température peut-elle être due à une variation azimutale du plasma, puisque qu'Ulysse ne suit pas vraiment une ligne de champ mais reste sur une coquille magnétique en balayant 90° de longitude (voir Annexe A.1) ? Pour cela, il faudrait exhiber une asymétrie de longitude «taillée sur mesure» qui fournisse une variation de température d'un facteur 4 sur 45° de longitude et qui soit adéquatement symétrique de part et d'autre de l'équateur centrifuge. Ce serait une interprétation singulièrement ad hoc et pour laquelle on est bien incapable d'avancer la moindre justification physique. Qui plus est, les variations azimutales effectivement observées [Thomas, 1993, revues dans,], [Desch, Farrell and Kaiser, 1994, et pour Ulysse :,], correspondent soit à des structures beaucoup plus étroites, de l'ordre d'au maximum 20° de longitude (simulées en tenant compte de la diffusion radiale et connues sous le nom de «doigts» de plasma [Yang et al., 1992], soit à des variations sur 180° mais modérées (en fait des variations de brillance aboutissant à des variations de température de l'ordre d'au maximum 20% pour les électrons du tore chaud [Schneider et al., 1997, par ex.,]), variations qui n'ont évidemment aucune raison d'être miraculeusement symétriques par rapport à la longitude à laquelle Ulysse a rencontré l'équateur centrifuge.

2) Peut-il y avoir une confusion entre diverses températures, due à la méthode de mesure elle-même, en présence notamment de distributions d'énergie non purement maxwelliennes (entre électrons chauds et froids par exemple, dans le cas d'une distribution type coeur + halo)? Un élément de réponse est donné dans le premier article présenté (ici ) où on montre que la température effectivement obtenue par notre méthode est reliée aux températures d'une somme de populations maxwelliennes de densités par :

Cette température mesurée est donc principalement celle des particules froides de la distribution. Si on modélise le tore avec deux espèces d'électrons (coeur + halo) [Bagenal, 1994, comme dans ,], c'est bien la température des électrons froids qu'Ulysse voit croître avec la latitude sur la figure iv.1, et c'est effectivement contradictoire avec l'hypothèse de l'équilibre diffusif isotherme de chaque espèce le long des lignes de champ.

Outre l'augmentation importante de la température avec la latitude, la comparaison densité/température laisse apparaître une forte anticorrélation entre ces quantités (le taux de corrélation vaut -0.87), bien visible sur la figure iv.1. Cette anticorrélation se traduit par l'existence d'une loi d'état empirique, dite loi polytrope:

à indice polytrope puisqu'il s'agit d'une anticorrélation.

  
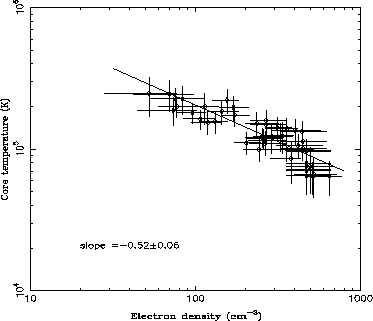
Figure iv.2: Température/densité électroniques mesurées in situ sur Ulysse, avec la meilleure droite de régression linéaire sur une échelle log-log (et tenant compte des barres d'erreurs dans les deux directions [Numerical Recipes, 1992]). Les données couvrent environ autour de l'équateur centrifuge. (La longitude varie d'environ 90° autour de 310° ouest (CML) et la distance à Jupiter varie peu, de 7.1 à 8.4 ).[extrait de Meyer-Vernet, Moncuquet and Hoang, 1995]

Pour calculer cet indice, on détermine la pente de la meilleure droite de régression linéaire de en fonction de (figure iv.2), ce qui donne : .

Après avoir soupçonné un artefact dû aux conditions ou à la méthode de mesure , on peut maintenant légitimement se demander comment peut perdurer un tel déséquilibre thermodynamique (i.e. une loi polytrope à ) dans un plasma supposé fluide, c'est-à-dire a priori soumis à de nombreux processus d'interaction entre particules (collisions et autres) qui devraient le faire relaxer vers l'état d'équilibre (on dira par la suite plus rapidement «thermaliser»).

En réalité, ce plasma est très peu collisionnel dans la région qui nous préoccupe ici et les libre-parcours moyens des particules sont très grands devant les échelles de hauteur des variations des densité et température électroniques qui nous intéressent : avec la plus grande densité et la plus petite température mesurées ici ( cm et K), le libre-parcours moyen des électrons froids (pour les collisions coulombiennes entre électrons) est . Comme le libre-parcours moyen augmente en s'éloignant de l'équateur centrifuge, et est encore plus grand pour les suprathermiques. Les autres libre-parcours (ions-électrons chauds, ionisation et excitation, recombinaison) sont du même ordre de grandeur [Book, 1986, p.32 de,] (et les libre-parcours moyens des ions sont encore plus grands [Strobel, 1989, ,]). Ces valeurs sont donc plusieurs fois plus grandes qu'une échelle de grandeur caractéristique de notre variation de densité et température (typiquement ou 7° de latitude pour que la température double et la densité soit divisée par 4). En d'autres termes, le temps que met une particule pour se déplacer le long d'une ligne de champ est très court comparé aux temps caractéristiques des interactions (au sens le plus large) des particules du plasma. C'est vrai aussi si l'on compare le mouvement le long des lignes de champ -qui détermine le confinement vertical du tore, et dont les échelles de temps caractéristiques vont de quelques secondes pour les électrons à quelques heures pour les ions les plus massifs- au mouvement de dérive des particules perpendiculairement à -qui détermine la diffusion radiale du tore, et dont l'échelle de temps caractéristique est de l'ordre de 2 mois [Cheng, 1986, par ex.,].

Avec de tels libre-parcours moyens, il paraît effectivement plus pertinent d'utiliser une approche microscopique cinétique du plasma, c'est-à-dire de décrire celui-ci par la donnée explicite d'une fonction de distribution de vitesses pour chaque espèce de particules. On déduit dans ce cas les quantités macroscopiques traditionnelles, comme la température, du calcul des moments de cette fonction de distribution. On sait qu'un plasma à l'état d'équilibre est alors décrit par une distribution de vitesses de Maxwell-Boltzmann (maxwellienne) isotrope qui a la forme normalisée (pour une densité n et une température T de particules de masse m) suivante:

 

où désigne la constante de Boltzmann. Dans ce cas, il est bien connu (on verra exactement pourquoi en IV.2) que la température reste constante le long des lignes de champ, en contradiction de même avec la mesure obtenue par Ulysse.

Notre résultat est aussi incompatible, c'est peut-être moins connu, avec une description cinétique du plasma fondée sur une distribution bi-maxwellienne, c'est-à-dire anisotrope et maxwellienne dans chacune des directions parallèle et perpendiculaire à , de la forme normalisée suivante:

Dans ce cas, notons tout d'abord que la température mesurée par Ulysse est la température perpendiculaire à et montrons brièvement que le sens de l'anisotropie «mesuré» (ou couramment admis [Sittler and Strobel, 1987, par ex. ,]) dans le tore d'Io ( ) produirait une décroissance de avec la latitude; on peut établir [Chiu and Schulz, 1978, Huang and Birmingham, 1992] en effet qu'en considérant une distribution bi-maxwellienne des vitesses, la température parallèle va demeurer constante le long des lignes de champ tandis que la température perpendiculaire devient (à l'abscisse curviligne s le long de la ligne de champ) :

 

où dénote l'anisotropie à l'équateur centrifuge.

Dans un champ poloïdal, la magnitude s'accroît le long de la ligne de force du champ , i.e. , et on voit alors facilement d'après iv.5 qu'en supposant l'anisotropie dans le tore d'Io (comme tout le monde l'affirme), on aura HB , et la température devrait diminuer avec la latitude. De plus, même en contestant le consensus des spécialistes du tore et en inversant donc le sens de cette anisotropie (i.e. ), on obtient, toujours d'après iv.5 : HB ; ce qui signifie que cette variation de température, due aux forces miroir-magnétiques, est nécessairement inférieure à celle de B le long d'une ligne de champ, c'est-à-dire assez faible dans la gamme de latitude explorée ici (quelque 15% sur 10° de latitude) , sans commune mesure avec la variation réellement observée.

Ainsi, une description microscopique du plasma usant d'une distribution de vitesses des électrons maxwellienne ou bi-maxwellienne ne nous permet pas davantage d'expliquer les résultats présentés sur la figure iv.1. Cela n'est pas trop désappointant puisque, comme on l'a vu, le milieu est a priori trop peu collisionnel pour relaxer vers une distribution maxwellienne. Qui plus est, la présence (avérée [Sittler and Strobel, 1987]) d'une population d'électrons suprathermiques au voisinage de l'équateur du tore montre que le plasma n'est déjà pas à l'équilibre thermique à l'équateur, et n'a pas de raison de thermaliser sur des distances telles que celles explorées par Ulysse de part et d'autre de cet équateur (2 à 3 rayons joviens), puisque les libre-parcours moyens (qui croissent en ) sont encore plus grands pour ces électrons suprathermiques que pour le gros des électrons. On va voir que cette absence intrinsèque d'équilibre thermique local dans les plasmas spatiaux sans collision, dont l'importance a été soulignée pour la première fois par [Scudder and Olbert, 1979] à propos du vent solaire, sera en fait la seule hypothèse nécessaire pour expliquer les variations observées de et avec la latitude dans le tore de plasma d'Io, y compris leur anticorrélation.