La figure vi.4, et les figures B.3 &
B.6 en annexe B.3,
résument la confrontation de notre nouveau modèle
aux mesures in situ de densité électronique
réalisées par Voyager 1 à l'émersion et Voyager 2 et Ulysse.
Sur ces trois figures, sont toujours rappelées dans le cartouche du haut à gauche,
les densités électroniques mesurées par Voyager 1 à l'immersion (trait fin)
et qui servent de références (point-tiret-point),
ou d'entrées si l'on préfère, au code de calcul.
Le trait tireté représente
l'extrapolation des densités à l'équateur centrifuge et le trait gras
le résultat du calcul du code sur la trajectoire de Voyager 1 (et qui
doit donc redonner une valeur proche des entrées initiales, l'écart permettant
d'estimer le degré de précision du code). Notons que chacun des profils
prédictifs est indiqué sur chaque cartouche par un trait gras (les
données étant soit représentées par des losanges pour Ulysse, soit par un trait
fin continu pour les autres cas). Ces profils sont calculés pour un choix donné
d'un kappa et d'une anisotropie, identiques pour tous les ions et indépendants
de la distance radiale, puis superposés aux données tels quels, sauf
pour Ulysse où l'on ajuste le profil calculé par un facteur multiplicatif
constant (i.e. on
autorise une translation sur l'échelle (log) des densités)
qui permet de tenir compte d'un «remplissage» absolu du tore
différent entre l'époque de Voyager 1 et celle d'Ulysse. Le champ magnétique
utilisé pour les obtenir est 
sans lame de courant (sauf la figure
B.6 à distribution bi-maxwellienne où on a utilisé,
pour permettre la comparaison avec [Bagenal, 1994], 
+ lame de courant).
le confinement vu par Ulysse
On a déjà largement défloré ce résultat dans la section précédente,
où l'on a remarqué
qu'on obtenait un confinement satisfaisant avec notre compromis
( 
) (figure ci-contre, où le modèle est «rehaussé»
pour les données d'Ulysse d'un facteur 1.9)
tandis que ce confinement était
insuffisant avec le même kappa mais une distribution isotrope
(figure B.3), et qu'enfin ce confinement était réalisable avec
une bi-maxwellienne mais dotée d'une anisotropie effarante
de 10.
Voyager 1 à l'émersion
On obtient pour Voyager 1 à l'émersion, quel que soit le kappa ou l'anisotropie, un résultat dont les gradients sont corrects mais avec un écart systématique des valeurs absolues de la densité; cela peut être dû à une asymétrie azimutale du tore de plasma, les longitudes joviennes balayées entre l'immersion et l'émersion étant approximativement décalées de 180°. Ce décalage entre prédiction et mesures à l'émersion (qui sont de moins bonne qualité qu'à l'immersion [Sittler and Strobel, 1987, ,]) est d'ailleurs constaté (quoique moins important) aussi bien en utilisant le modèle de [Bagenal, 1994] que celui de [Divine and Garrett, 1983] [Hoang et al., 1993, par ex. figure 3 de ,].
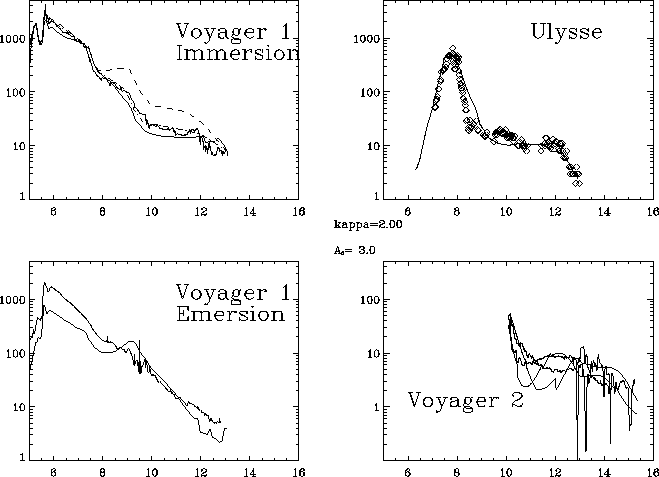
Figure vi.4: Confrontation du modèle aux mesures de densité électronique de Voyager
1 à l'émersion, de Voyager2 et d'Ulysse, avec
( on a aussi représenté la mesure de
Voyager 1 à l'immersion qui sert de référence pour la variation radiale).
Les densités d'Ulysse et de Voyager 2 dans la banlieue du tore
À conditions de ne pas utiliser un modèle de champ avec lame de courant,
les niveaux de densités électroniques obtenus à l'extérieur du tore
(et à hautes latitude -voir éphémérides en annexe A.1), disons
au delà de 9 
, sont assez bien prédits par notre modèle, aussi bien sur
Ulysse que sur Voyager 2. Sur les données de Voyager 2, aucun
facteur de remplissage n'est appliqué et le pic de densité prévu
à la plus petite approche de Voyager 2 est parfaitement prédit. On obtient
une prédiction encore meilleure sur la figure B.3 à l'aide
d'une distribution kappa isotrope ( 
), tandis qu'on obtient
une très mauvaise prédiction avec la bi-maxwellienne fortement anisotrope
(ce qui laisse penser qu'à ces distances, l'anisotropie n'est sûrement
pas considérable , voir note 12).
Concernant les données d'Ulysse, et
en appliquant le facteur de remplissage de 1.9 pour obtenir un bon ajustement
prés de l'équateur, on obtient une prédiction correcte des niveaux de densité
électronique mesurés dans la partie la plus externe du tore explorée par
Ulysse. Comme on l'avait
annoncé (note 7), entre 9 et 10 , la densité observée est légèrement
plus importante que celle prédite, bien que le modèle prenne déjà en compte
à l'équateur centrifuge une légère augmentation des densités observées par
Voyager 1 (entre autres modifications, comme la composition et
les températures), ces modifications des paramètres du tore
étant généralement attribuées à la présence d'Europe .
On peut donc affirmer
que, bien qu'il ne fût pas équipé pour explorer la magnétosphère
de Jupiter , Ulysse a confirmé
cette influence d'Europe sur le tore de plasma d'Io, sinon détecté
un «tore d'Europe», ce qui était malheureusement hors de sa portée.