La nécessité d'un nouveau modèle, au moins pour la structure latitudinale du tore d'Io, est évidente dès lors que les modèles disponibles reposent sur une hypothèse incompatible avec des observations nouvelles, en l'occurrence celles d'Ulysse sur la variation de température avec la latitude. Il serait en effet fâcheux de continuer à utiliser les anciens modèles de densité 2-D (par rapport à la latitude centrifuge et à la distance radiale) sans vérifier s'ils sont peu ou prou affectés par la nature des distributions d'énergie utilisées pour les calculer. À cet égard, l'ébauche de modèle à distribution kappa proposé dans [B.1] nous suggère que les profils de densité, «d'allure kappa», vont sensiblement différer des classiques profils gaussiens dont nous avons l'habitude.
Cette nécessité d'un nouveau modèle de densité en latitude se justifie aussi
tout bonnement
par la mauvaise capacité de prédiction des modèles disponibles, fondés sur les
observations de Voyager 1, des densités mesurées in situ par les autres sondes.
On montre par exemple sur la
figure v.1 la mauvaise adéquation du modèle de [Bagenal, 1994]
(en utilisant plusieurs configurations possibles de ce modèle) aux mesures de
densité effectuées par Ulysse dans le tore et sa banlieue.
[Hoang et al., 1993, Moncuquet et al., 1997].
On constate que, tenant compte du feuillet de plasma ou pas pour le modèle de
champ et tenant compte d'une forte anisotropie des ions suprathermiques ou pas
(comme le permet le modèle de [Bagenal, 1994]), on ne peut pas modéliser
correctement le fort confinement du tore et notamment la chute très rapide de
densité observée par Ulysse à l'émersion (côté hémisphère Sud), même si les
niveaux de densité prédits dans la banlieue du tore (au delà de 10 
) sont
relativement corrects 
.
Même en changeant le niveau absolu des densités (autrement dit «en
remplissant» le tore) tout en conservant le gradient équatorial de densité
observé par Voyager 1 qui sert de référence dans le modèle de Bagenal, on ne
changerait rien à cela, sinon qu'on prédirait alors au delà de 10 des
densités beaucoup trop élevées.
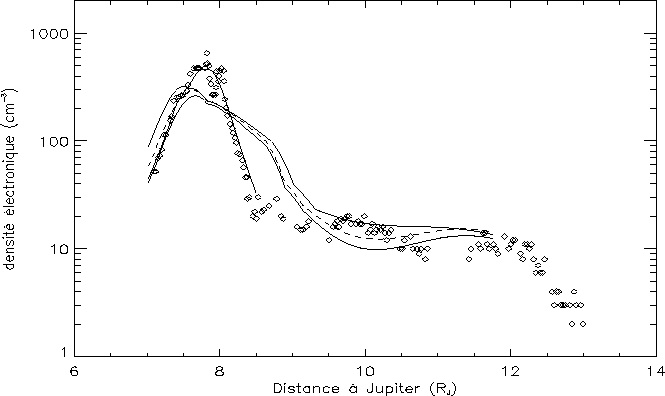
Figure v.1: Toutes les densités électroniques obtenues avec Ulysse comparées
à quelques profils théoriques. Les deux courbes en trait fin qui encadrent la
courbe en tirets sont les profils de densité calculés à partir du modèle de
Bagnal [1994] avec un champ 
sans lame de plasma et une distribution
isotrope (courbe du haut) ou avec un champ , une lame de plasma et une
anisotropie du halo égale à 5 (courbe du bas). La courbe en tirets est
intermédiaire entre ces cas ( + lame de plasma et isotrope)
[NB: la différence entre utiliser le modèle de champ magnétique 
ou
pour calculer ces profils est complètement négligeable à ces distances]. La
courbe en trait gras, limitée au domaine de validité de la loi polytrope (à
) est le profil déduit de l'ébauche de modèle
"d'allure kappa" [Meyer-Vernet, Moncuquet and Hoang, 1995]
qui est montré en 2-D sur la figure IV.3 .
Évidemment, devant ce constat d'échec entre prédictions et observations, une attitude consiste à dire que le tore a changé et change en permanence, chaque observation constituant un cas particulier accidentel, et que les différences entre les observations d'Ulysse et de Voyager 1 sont purement météorologiques (ou temporelles), et/ou liées à des variations azimutales dont nous ignorons tout, ce qui clôt le sujet. Une autre solution, moins défaitiste, consiste à tenter de comprendre ce qu'il y a de permanent et de stable dans le tore de plasma d'Io, même avec le peu de mesures in situ dont nous disposons : si nous réussissons par exemple à expliquer conjointement les mesures de Voyager 1 et d'Ulysse via un modèle cinétique, et même s'il nous manque des paramètres (kappa et anisotropies réels des ions) qu'il nous faudra arbitrairement fixer, cela prouvera qu'une «certaine» structure du tore perdure, notamment une structure radiale à l'équateur, et que celle-ci doit être explicable indépendamment du temps qu'il fait sur Io ou sur Jupiter. C'est assurément un des enjeux d'une nouvelle modélisation de la structure latitudinale du tore.
Un autre enjeu d'une nouvelle modélisation serait de répondre à quelques problèmes ouverts (qui sont très nombreux) posés par l'existence et la pérennité de cet objet céleste.
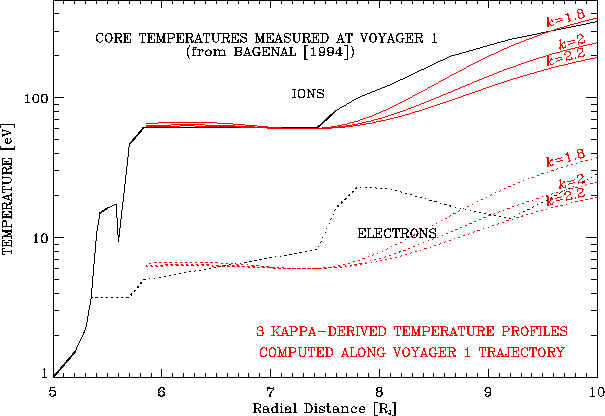
Figure v.2: Profils de température le long de la trajectoire de
Voyager 1, calculés
en utilisant l'ébauche de modèle "kappa" (non isotherme avec la latitude)
présenté section IV.3 pour 3 valeurs du kappa.
On a supposé la température à l'équateur centrifuge constante
après 
(60 eV pour les ions et 6 eV pour les électrons) et la
variation de température ainsi calculée ne dépend que de la variation de
latitude de Voyager 1 .
Les profils en noir sont une sélection des mesures de Voyager 1 (inbound)
et constituent la base de référence du modèle de
Bagenal [1994]. (Figure extraite de Moncuquet [1995])
Dans cet ordre d'idées, et comme notre «approche du tore»
se limite grosso modo à
l'étude des
conséquences sur la structure latitudinale du tore de la mise
en cause de l'équilibre thermique local du plasma,
on peut notamment se demander si des variations des températures
observées ça et là ne sont pas dues, comme sur Ulysse pour la température
des électrons, à des variations en latitude centrifuge de la sonde
qui a mesuré ces températures.
À cet égard, il est particulièrement troublant que la température
des ions mesurée par Voyager 1, qui sert de référence pour le calcul du modèle
de [Bagenal, 1994], augmente sensiblement à partir d'environ 7.5 (voir figure
v.2); cette distance correspond grosso modo au moment où Voyager 1
commence «à décoller» de l'équateur centrifuge
(voir figure i.2 ou iv.3, côté immersion).
On a d'ailleurs calculé et dessiné sur la figure v.2 les profils de
température obtenus avec notre modèle primitif [B.1] et un
modèle aussi très simplifié de champ
magnétique (dipôle incliné de 10°) pour calculer l'équateur centrifuge, en supposant la température des
ions constante à l'équateur centrifuge. Vu la grossièreté des hypothèses, les
profils «kappa-like» montrés sur cette figure ne sauraient être
que qualitatifs,
mais indiquent assurément que cette piste des
distributions non-thermiques des ions est à explorer sérieusement (ce sera fait
dans la section suivante), en particulier
pour tenter d'expliquer la variation des températures des particules
sur Voyager 1 (ce sera fait au chapitre vi).
Cette figure v.2 a été présentée en octobre 1995 au colloque du
DPS. Plus récemment,
[Thomas and Lichtenberg, 1997], en utilisant notre ébauche de modèle (mais exprimé
en fonction de l'indice polytrope au lieu du kappa) et en supposant
que la température à l'équateur décroissait en 
[Herbert and Sandel, 1995], sont arrivés à la même conclusion concernant
l'intérêt de cette piste: c'est dire s'il est grand'temps d'en faire un
boulevard.