Distributions bi-kappa anisotropes des ions

Sur Ulysse, les distributions de vitesses des ions n'ont pas été mesurées; elles ne peuvent pas non plus être déterminées sans ambiguïté à partir des données de Voyager 1 parce qu'entre autres problèmes, les spectres de chacune des espèces d'ions reconnues dans le tore ( , , , et ) n'ont pu être complètement discriminés. Toutefois, ces données indiquent que les distributions n'étaient pas maxwelliennes [Bagenal and Sullivan, 1981] et les modèles théoriques impliquent des distributions de vitesses des ions fortement non-thermiques [Smith and Strobel, 1985]. De plus, les libre-parcours moyens des ions (qui sont environ 10 fois plus chaud que les électrons -voir figure v.2) sont encore plus grands que ceux des électrons, et cela plaide en faveur d'une moins grande efficacité des processus de thermalisation des ions par rapport aux électrons. Comme on a vu grâce à Ulysse qu'on ne pouvait pas supposer les électrons à l'équilibre thermique local, il paraît raisonnable d'envisager cette possibilité pour les ions.

L'idée est donc ici de modéliser les distributions de vitesse des ions par des fonctions kappa, mais en s'affranchissant des hypothèses utilisées dans notre première ébauche de modèle (voir iv.3 ou annexe B.1), à savoir d'une part, l'égalité des kappa des ions et des électrons, qui est franchement arbitraire et d'autre part, la composition physico-chimique à un seul ion, qui est franchement fausse. Avec ce qu'on a déjà établi au chapitre iv, des profils de densités isotropes pourront être calculés en utilisant des équations de la forme (iv.13), avec un potentiel pour les électrons et pour les ions de charge Ze, étant le potentiel centrifuge dû à la corotation; la difficulté supplémentaire par rapport au calcul mené dans [B.1] sera de résoudre le système formé par ces 9 équations (celles des électrons + celles des 8 ions cités ci-dessus) à 10 inconnues (les densités et le potentiel électrostatique ambipolaire ), auquel on ajoutera l'équation de neutralité du plasma (incluant une composition physico-chimique qui peut varier avec la distance). On en profitera également pour calculer le potentiel centrifuge plus précisément, c'est-à-dire en se dotant du modèle de champ magnétique le plus performant sur le marché.

Ce programme est sans doute bel et bon, mais il serait dommage de s'y atteler sans en profiter pour introduire une anisotropie des températures (en particulier des températures des ions) relativement aux directions parallèle et perpendiculaires au champ magnétique (ou, ce qui est équivalent, de prendre en compte les forces miroir-magnétiques, non négligeables aux hautes latitudes). Comme on l'a remarqué à plusieurs reprises, on a malheureusement pas de mesures fiables des températures parallèles dans le tore de plasma d'Io. Néanmoins, on a de bonnes raisons de penser qu'une anisotropie de température existe (surtout pour les ions) dans le tore de plasma d'Io à cause du mécanisme d'assimilation (pick-up) local des neutres [Siscoe, 1977].

Rappelons brièvement ce mécanisme : un neutre est ionisé et soudainement entraîné à la vitesse de corotation du plasma en tournant autour des lignes de force du champ magnétique. Dans la direction perpendiculaire au champ magnétique, les vitesses des ions ainsi assimilés vont être distribuées gyrotropiquement avec une importante vitesse d'ensemble égale à la vitesse de corotation au lieu d'assimilation du neutre. Dans la direction parallèle, les particules assimilées ont au départ une vitesse d'ensemble grande dans le repère lié au plasma (la composante parallèle à de la différence entre la vitesse des neutres et la corotation) qui va avoir tendance à relaxer par instabilité faisceau plasma. Il peut exister aussi un apport d'énergie cinétique lié à l'inclinaison du champ magnétique sur l'axe de rotation de Jupiter (voir i.1.1) et au gel du champ dans le plasma mais cet apport est faible devant l'énergie cinétique acquise dans la direction perpendiculaire du fait de la corotation. On prévoit donc, pour ces particules fraîchement assimilées des distributions de vitesses «en anneau», dont on trouve des exemples plus ou moins compliqués dans la littérature [Barbosa et al., 1985, voir pour un exemple compliqué,], mais qu'on n'a jamais mesurés in situ dans les plasmas spatiaux. Cependant, les temps d'isotropisation des ions étant relativement grands , on peut penser qu'une certaine anisotropie de température pourra perdurer.

Pour obtenir un modèle de structure latitudinale du tore, on veut donc généraliser l'effet de filtration des vitesses, expliqué au chapitre iv, à des distributions kappa anisotropes [Summers and Thorne, 1992, voir pour une expression formelle de ces distributions,], que nous appellerons «bi-kappa», par analogie avec les bi-maxwelliennes, et qui s'écrivent (normalisées):

 

En appliquant le théorème de Liouville avec conservation de l'énergie, comme dans le cas isotrope, et en ajoutant la conservation du moment magnétique , on va pouvoir déduire le profil de densité pour chaque espèce de particules. Rappelons que le théorème de Liouville permet d'exprimer la conservation de la distribution à l'abscisse curviligne s le long de la ligne de champ depuis l'équateur centrifuge, ce qui donne, en présence d'un potentiel attractif monotone , d'un champ de magnitude B(s) et compte-tenu des invariants cités :

 

en remarquant que :

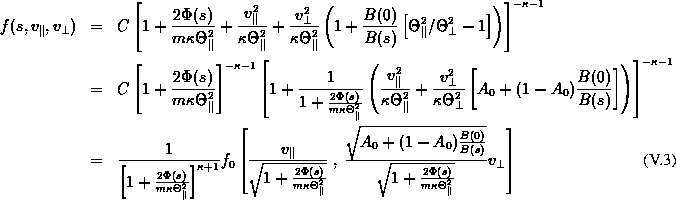
où est le facteur d'anisotropie à l'équateur centrifuge (et où C est la constante de normalisation de v.1). Cette équation généralise la relation générique iv.11 au cas anisotrope.

En utilisant cette relation pour le calcul des moments d'ordre 0 et 2, on en déduit les profils de densité et températures suivants :

   

Notons qu'avec ces distributions bi-kappa, ni la température parallèle ni la température perpendiculaire ne vont suivre strictement une loi polytrope en le long des lignes de champ, la température perpendiculaire subissant un effet supplémentaire, dû à l'existence d'une anisotropie de température à l'équateur (en d'autres termes, cette anisotropie de température n'est pas conservée le long des lignes de champ). Cet effet sera évidemment d'autant plus négligeable que la variation de la magnitude du champ est faible (elle est d'au maximum 20% sur nos mesures d'Ulysse) et/ou que l'anisotropie à l'équateur est faible (l'amplitude de cette anisotropie reste un mystère, à part pour les électrons : on doit donc pouvoir la supposer grande dans les modèles). Lorsque , on retrouve le modèle bi-maxwellien anisotrope de [Huang and Birmingham, 1992] déjà explicité précédemment (équation iv.5). Lorsque (isotropie), on retrouve le profil de (iv.13) introduit par [Meyer-Vernet, Moncuquet and Hoang, 1995](annexe B.1).

Il ne reste plus qu'à réaliser le programme décrit préalablement (v.2), c'est-à-dire résoudre un système formé par 9 équations du type de v.4 écrites pour chacune des espèces détectées dans le tore, en se donnant en entrée les n(0) et , autrement dit un profil de référence à l'équateur centrifuge, et en choisissant divers et : ce sera l'objet du chapitre vi.

Avant cela, on veut illustrer dans un cas simple (un seul ion) et en s'intéressant uniquement au confinement n(s)/n(0), ce que donne la résolution de ce type d'équation v.4, notamment les effets qualitatifs de la variation des paramètres kappa et d'anisotropie.

  
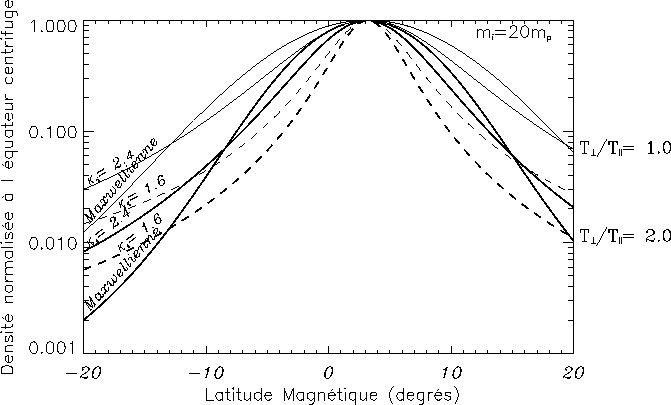
Figure v.3: Densité de plasma (normalisée à l'équateur centrifuge) en fonction de la latitude magnétique (modèle dipolaire du champ jovien), pour deux valeurs du kappa (1.6 et 2.4) de la distribution d'énergie d'un ion "moyen" du tore ( ), comparé au profil obtenu avec une distribution maxwellienne ( ). Les profils obtenus avec une distribution isotrope sont en traits fins, les profils obtenus avec une anisotropie de température ( ) sont en gras. Le kappa des électrons est fixé à 2.4 [Meyer-Vernet, Moncuquet and Hoang, 1995] et l'anisotropie à 1.2 [Sittler and Strobel, 1987]

On a représenté sur la figure v.3 plusieurs profils de densité normalisés à l'équateur centrifuge, dans le même plan méridien que la figure i.1 et pour un dipôle incliné d'environ 10° sur l'axe de rotation jovien, en fonction de la latitude magnétique (ce qui explique que les profils soient décalés d'environ 3°, qui est l'écart entre l'équateur centrifuge et magnétique dans ce plan méridien -voir légende de i.1). Ces profils sont obtenus par la résolution de 2 équations de type v.4 avec l'équation de neutralité qui s'écrit dans ce cas et permet d'éliminer des équations le potentiel électrique ambipolaire . On voit sur cette figure que les distributions kappa, utilisées pour obtenir les profils de densité, ont tendance à confiner davantage les particules près de l'équateur, en comparaison de ce que donne une maxwellienne, mais à prédire un peuplement plus important aux grandes latitudes. L'effet de l'anisotropie est, quelle que soit la distribution (bi-kappa ou bi-maxwellienne), celui d'un fort confinement à l'équateur centrifuge; mais la différence notée dans le cas isotrope kappa/maxwellienne demeure, c'est-à-dire qu'à anisotropie fixée, les bi-maxwelliennes ont tendance à raréfier davantage le plasma aux hautes latitudes que les bi-kappa. Ces effets se retrouveront grosso modo dans les prédictions et comparaisons aux mesures in situ du modèle de structure 2-D complet que nous allons présenter et utiliser dans le chapitre suivant.