Les températures et densités qui vont servir de point de départ à notre
modèle sont
exactement celles utilisées par [Bagenal, 1994] pour calculer son
modèle jusqu'à 10 
, c'est-à-dire
48 points (de 4 à 12 ) sélectionnés parmi les mesures de
Voyager 1 à l'immersion
.
Ces paramètres (pour les principales espèces) sont repris synthétiquement
(dans un plan méridien, en fonction de la distance de Voyager 1 à Jupiter
à l'acquisition) sur la figure vi.1.
Notons que ces mesures de références incluent une composition physico-chimique
(pourcentage des différentes espèces) dont on sait qu'elle n'est qu'un
compromis possible. D'autre part, la température
des électrons mesurée par Voyager 1 prête sérieusement à caution, le potentiel
flottant de la sonde étant très fluctuant, notamment entre 7.5 et 9
[Sittler and Strobel, 1987, ,]. Néanmoins, ces paramètres (composition précise et
température électronique) ne sont pas très influents sur la structure
latitudinale qui nous occupe, celle-ci étant principalement «contrôlée» par
la pression totale des ions. Ces réserves faites, je renvoie le lecteur à
[Bagenal, 1994] [et à ses références bibliographiques] pour la revue des
paramètres du tore issus de Voyager 1 montrés sur la figure vi.1.
En résumé, mon nouveau modèle utilise, concernant la structure radiale du tore, les mêmes «entrées» que celui proposé par [Bagenal, 1994], et peut à cet égard être considéré comme une généralisation/adaptation de ce modèle, cette adaptation ayant principalement pour but d'affranchir le modèle de l'hypothèse d'équilibre diffusif isotherme (infirmée par Ulysse). Pour ce faire, on calcule la structure en latitude à partir de la structure radiale empirique à l'équateur centrifuge, en utilisant les nouveaux profils de confinement liés aux distributions bi-kappa (Éq.v.4) qui ne supposent pas cet équilibre thermique local espèce par espèce (et on obtient aussi «en prime» des profils latitudinaux des températures en usant des équations v.5&v.6).
Ceci dit, l'extrapolation de ces paramètres «choisis», obtenus par Voyager
1 (à l'immersion), à des paramètres de référence à l'équateur centrifuge
va d'emblée dépendre du modèle de confinement le long des lignes de champ
qu'on utilise, puisque, rappelons-le, Voyager 1 ne reste pas exactement dans
cet équateur centrifuge (et s'en éloigne même significativement au delà de 7.5
-voir annexe A.1). Ces paramètres à l'équateur centrifuge, dont le calcul
constitue la première étape de la construction d'un modèle 2-D, seront donc
différents entre le modèle de Mme Bagenal et le mien. On a représenté sur la
figure vi.2 les densités et les températures obtenues
à l'équateur centrifuge, à partir
des données de Voyager 1 (figure vi.1), en utilisant un profil de
structure «bi-kappa», c'est-à-dire donné par les équations
v.4,v.5,v.6, avec 
, 
pour les
ions et quelle que soit la distance radiale.
Remarquons tout d'abord que, sur cette figure vi.2,
les densités des différentes espèces
présentent des profils à l'équateur centrifuge notablement différents
de ceux obtenus par F. Bagenal
[Bagenal, 1994, voir Figure 5& 6 de ,].
Ces différences s'accroissent
avec la latitude centrifuge de Voyager, notamment après 8 , ce qui est
évidemment explicable par la différence entre les confinements prédits par un
modèle «bi-kappa»
anisotrope et ceux prédits par un modèle supposant l'équilibre
diffusif
isotherme. En particulier, le confinement
étant plus fort dans le modèle bi-kappa (voir figure v.3), on
récupère en retour des densités plus élevées. En particulier, on renforce à
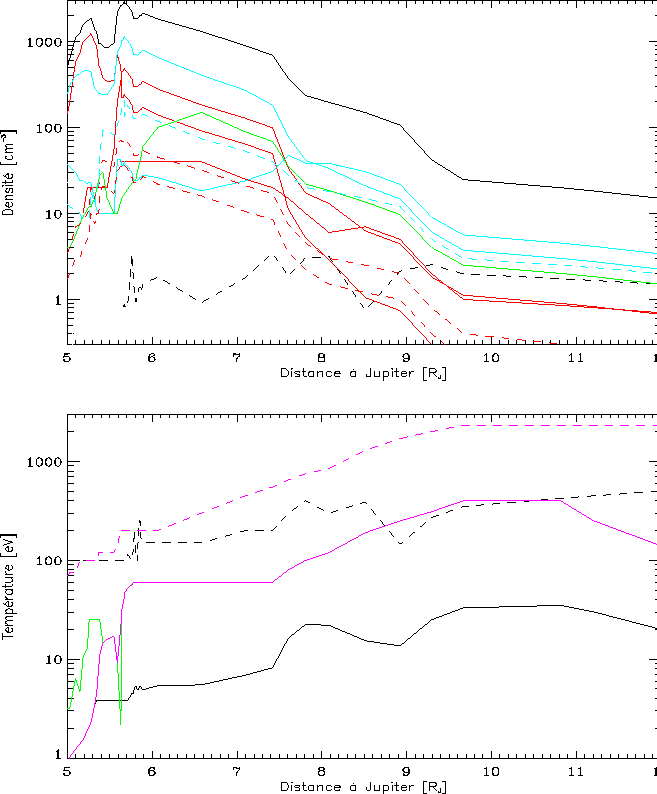
Figure vi.1: Les densités et les températures de référence (mesurées par Voyager
1) utilisées en entrée du code, pour les principales espèces d'ions. Ce sont
celles du modèle de Bagenal[1994]. Les paramètres relatifs aux espèces froides
(coeurs) sont en traits continus, ceux relatifs aux espèces chaudes (halos) en
tirets. Les densités et températures des électrons sont en noir, les densités
des ions S ( 
) en rouge et celles des ions O ( 
) en bleu;
la densité des protons est indiquée en vert (figure du haut). Les températures
de toutes les espèces d'ions sont identiques (sauf pour les protons entre 5 et
6 ) et indiquées en magenta sur la figure du bas.
l'équateur centrifuge l'effet de la légère augmentation du
gradient de densité totale observée aux alentours de 9
par Voyager 1, derrière une structure où la pente est plus
importante et qu'on appelle communément «la rampe» dans les descriptions
phénoménologiques de la structure
radiale du tore.
Depuis [Intriligator and Miller, 1982], cette partie extérieure du tore est
soupçonnée d'être partiellement alimentée par le satellite Europe
.
On verra (section vi.3) que
cette augmentation relative de la densité
totale du plasma vers 9 a été confirmée par
Ulysse.
Une autre différence, sans doute la plus lourde de conséquences,
entre nos extrapolations
des mesures de Voyager à l'équateur centrifuge et celles de [Bagenal, 1994]
concerne les températures des ions, qui varient avec la latitude
dans notre modèle, tandis qu'elles étaient constantes dans le modèle de Bagenal.
Cette comparaison des températures des figures vi.1 et vi.2
va faire l'objet de la discussion suivante.