Précisons tout d'abord que les températures représentées sur la figure vi.2 sont les températures effectives perpendiculaires définies par les moments de la distribution bi-kappa anisotrope (Éq.v.6); perpendiculaires car ce sont ces températures qu'a mesurées Voyager 1 et effectives car ce sont les températures les plus aisément comparables aux températures des populations froides (indiqué en trait continu sur la figure vi.1) d'une distribution de type coeur+halo.
En examinant ces profils de température
en fonction de la
distance radiale à l'équateur centrifuge, on
constate que
les températures évoluent différemment avec la distance selon leur espèce,
notamment à cause du filtrage des énergies différencié en
fonction des masses et des charges des diverses espèces
.
Cette évolution a lieu, comme
on s'y attendait, dans le sens d'une
loi polytrope à 
, c'est-à-dire des températures
plus faibles à l'équateur
centrifuge qu'aux latitudes où Voyager les a mesurées. La moyenne
(arithmétique) de ces températures est grosso modo constante avec la
distance radiale, ce qui laisserait penser que la diffusion radiale
dans le tore est plutôt isotherme,
mais, si on examine attentivement les températures des deux
espèces d'ions trouvées majoritaires vers 8.5 
(O 
,S 
,
en trait plus gras sur la figure vi.2)
on voit qu'elles décroissent avec la distance radiale
entre environ 7.5 et 9 , selon une loi de puissance
approximativement en 
(indiquée par un trait traversant de part en part la
figure vi.2) correspondant à une diffusion radiale
adiabatique telle que proposée par [Herbert and Sandel, 1995].
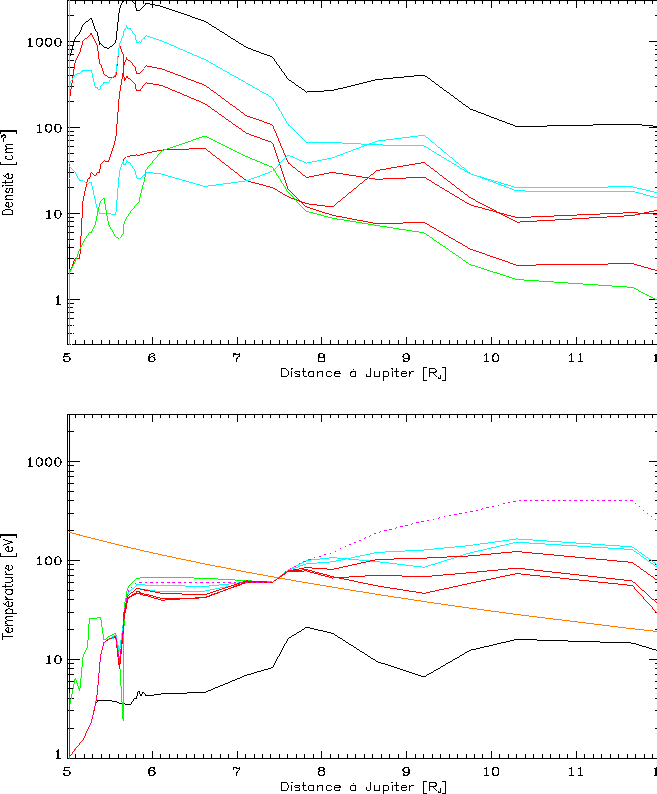
Figure vi.2: Les densités et les températures rapportées à l'équateur centrifuge à
partir de celles de références montrées figure VI.1, en utilisant des
fonctions bi-kappa pour modéliser les distributions d'énergies des particules
( 
pour tous les ions,
pour les électrons). Les conventions sont identiques
à celles de la figure VI.1, sauf qu'il n'y a plus d'espèces chaude ou
froide mais des densités totales (en haut) et des températures perpendiculaires
effectives (en bas) - (grosso modo comparables aux températures des froids des
distributions coeur+halo). On a superposé (pointillés) la température des ions
froids de la figure VI.1 et, en trait continu orangé, une variation
adiabatique des températures en .
Une conséquence importante est que notre modèle
rend aussi compatible le résultat
expérimental d'Herbert and Sandel, [1995], c'est-à-dire
la baisse des températures
parallèles avec la distance jovicentrique (déduite de l'observation de
spectres UV sur Voyager 1), avec l'augmentation
des températures perpendiculaires observée par le même Voyager 1 (mais par
les analyseurs de particules) à des distances jovicentriques supérieures à 7.5 rayons joviens.
En revanche, une baisse des températures parallèles des ions avec la
distance jovicentrique dans le tore d'Io est tout-à-fait incompatible avec le
modèle de [Bagenal, 1994] en l'état. Qui pis est, si l'on veut tenter d'expliquer
cette baisse des températures parallèles
en même temps que l'augmentation (observée par Voyager 1)
des températures perpendiculaires (fig.vi.1), par la simple introduction
d'une anisotropie des températures à l'équateur, tout en maintenant
l'hypothèse de l'équilibre thermique le long des lignes de champ (i.e.
en utilisant une distribution bi-maxwellienne [Huang and Birmingham, 1992]),
on prédira des températures perpendiculaires (et donc aussi parallèles)
à l'équateur centrifuge encore plus élevées, comme on l'avait déjà fait
remarquer (Éq.iv.5) et
comme on peut aussi le constater sur l'exemple obtenu avec une bi-maxwellienne
donné en annexe B.3 (figure B.4).
Notons pour terminer cette discussion que notre modèle à espèces multiples et à distribution bi-kappa anisotrope confirme le résultat préliminaire que nous avions montré au DPS en 1995 (voir figure v.2), mais pour lequel nous avions seulement utilisé une ébauche de modèle (i.e. kappa unique, une seule espèce d'ion et isotrope -voir annexe B.1) qui pouvait laisser craindre que le résultat obtenu soit dépendant des hypothèses par trop simplificatrices utilisées.